Typically these experiments use correlated (but spatially separated) photons or particles generated in an atomic decay process. These are each passed through a polarizer and the coincidence count rate in dependence on the relative orientation of the two polarizers is being measured. According to a theory expressed in Bell's Theorem (Bell's Inequality) this should yield different results for the 'Quantum Mechanics' and the 'Hidden Variables' assumption. All experiments are claimed to rule out the existence of Hidden Variables as Bell's Inequality is violated and the coincidence rate (for initially unpolarized radiation) is observed to follow the well known Malus law
(1) n(θ) = cos2(θ) ,
where θ is the angle between the two polarizers and n(θ) the relative coincidence count rate.In terms of classical optics this result can not be explained as in general a given direction of polarization has components along any set of two directions even if the latter are perpendicular to each other. For an initially unpolarized signal, one should therefore also expect a coincidence count rate for correlated emissions for θ = 90o, in contradiction to the experiments.
This circumstance has led physicists to the conclusion that in fact the physical property of 'polarization' does not exist objectively and independently but is only created by the polarizers when the light is transmitted by the latter. The requirement that the polarization in both channels should be identical (by virtue of the origin of the radiation) would then imply that for crossed polarizers no coincidence signal is detected. This has then led to the further interpretation that spatially separated events (e.g. as defined by the polarizers) can have some kind of non-local interaction beyond the known forces of interaction, which can cause physical objects to change state dependent on the physical state of another object an arbitrary distance away (entanglement). However, the flaw with the above argument is that the classical (Hidden Variable) interpretation assumes the light to be infinitely coherent i.e. it completely neglects the stochastic time dependence of the radiation field caused by the finite length of the light pulses and the incoherent superposition of emissions from different atoms. As follows from the semi-classical treatment on my site plasmaphysics.org.uk regarding Photoionization, the exact time of the photoelectron emission on detection depends on the time dependence of the radiation field i.e. the time dependences should ideally be identical in order to cause coincidences at the two detectors. As the original emissions in the two channels are strictly correlated by their very nature, this should in principle be naturally the case (at least if the size of the light source is much smaller than the coherence length of the emissions), but obviously after passing differently orientated polarisers this will in general not hold anymore as the individual atomic emissions are weighted differently: if the x-axis is chosen such that it bisects the two polarizers (which are rotated by an angle θ with regard to each other), the transmitted electric fields of a light pulse with original amplitude E1,0(t) and polarization angle φ(t) is
(2) E1(t) = E1,0(t) .[cos(φ(t)).cos(θ/2)+sin(φ(t)).sin(θ/2)] .
whereas for polarizer 2 the transmitted electric field is(3) E2(t) = E2,0(t) .[cos(φ(t)).cos(θ/2)-sin(φ(t)).sin(θ/2)] .
assuming that the initial polarization reaching polarizer 2 is identical to that at polarizer 1 (see the figure below for an illustration of the geometry)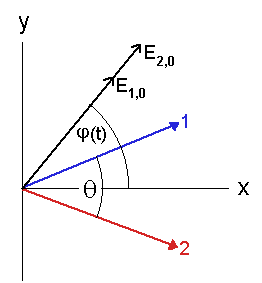
Geometry for the transmission of correlated light pulsesby two polarizers rotated by an angle θ
Now it is obvious from my Photoionization Theory that a simultaneous release of photoelectrons is only guaranteed if E1(t)= E2(t) which strictly speaking requires θ=0. For the case of 'coherent' photoionization (i.e. if the light intensity is high enough), the released photoelectrons might still register as simultaneous within the coincidence window for rotated polarizers, but this case is certainly not applicable to coincidence measurements as used for the Bell test experiments. The coherence time of the corresponding light pulses may be longer than that of sunlight for instance, but their intensity is certainly much smaller and thus the 'incoherent' case (i.e. a stepwise photoionization) is applicable. Now in this case, we have therefore the situation that the random energy increases for each light pulse will not be exactly correlated in the two channels unless θ=0. Otherwise there will be a component which becomes more and more anti-correlated the more the angle approaches θ=90o. This anti-correlation means that in general the accumulated energy after N light pulses can not be identical in both detectors unless it is by coincidence exactly equal to the statistical average N.<Δε> where N is the number of light pulses and (see the link above)
(4) <Δε> = e2/(2m) .τc2.<E2>
the long term statistical average of the energy increase Δε due to one light pulse (where e is the elementary charge, m the electron mass, τc the coherence time of the light pulses and <E2> the statistical average of the square of the electric fields of the light pulses as transmitted by the polarizers).In general however, the energy gained will deviate from the mean value by an amount which on average is given by the standard deviation <Δε>. √N. The anti-correlated component for non-parallel polarizers implies thus that if one channel is above the mean value by a certain amount, the other will be below it by the same amount, i.e. the photoelectrons in both channels could never be released simultaneously, or at least only with a very small probability (see diagram below)
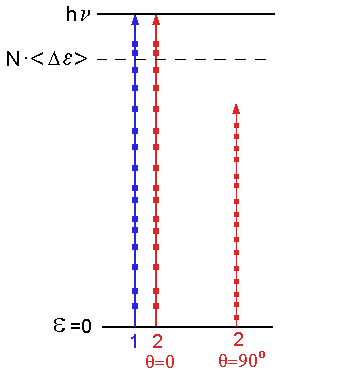Schematic illustration of photoionization processfor parallel and crossed polarizers
The dependence of the coincidence rate on the polarizer angle θ is obtained by considering the difference between the energy increases of the electrons in the two detectors. In general, the energy increment due to light pulse i is
(5) Δεi = e2/(2m) .τc2.Ei2 ,
i.e. the accumulated energy difference between the two channels is(6) Δε(θ) = Σi Δε1,i- Δε2,i = e2/(2m) . [ τc,12 .Σi E1,i2 - τc,22 .Σi E2,i2 ] .
With Eqs.(2) and (3) (where the index i replaces now the variable t) this evaluates to
(7) Δε(θ) =
e2/(2m) . (τc,12.E1,02 - τc,22.E2,02) .Σi [cos2(φi).cos(θ)+ sin2(θ/2) ] +
+ e2/(2m) .
(τc,12.E1,02 + τc,22.E2,02) .sin(θ) .Σi sin(φi).cos(φi) .
The second term on the other hand is due to the anti-correlated energy increases and the sum has a mean value of 0 with a standard deviation √N for a sequence of N light pulses with a stochastic distribution of polarization angles φi. This term is thus responsible for the angle dependence of the coincidence rate and, dropping the correlated components in this sense, we can write for the expectation value of the absolute value of the energy difference
(8) <|Δε|>(θ) = √N .e2/(2m) . (τc,12.E1,02 + τc,22.E2,02) .sin(θ) .
Now because of the random walk (diffusive) nature of the energy difference for the two detectors, the probability of finding the electrons with an energy difference small enough to enable a simultaneous release (i.e. smaller than <Δε> (Eq.(4)) depends on the square of <|Δε|>(θ), i.e. we can write for the probability of a coincidence not occurring (normalized to the value for orthogonal polarizers)(9) 1- n(θ) = <|Δε|>2(θ)/<|Δε|>2(90o) = sin2(θ) ,
and thus(10) n(θ) = cos2(θ) ,
i.e. the Malus law is obtained. It reflects thus merely the probability that the energy difference of the electrons in the two detectors remains within the required energy 'bandwidth' <Δε> (Eq.(4)), with the quadratic behaviour simply being due to the random walk (diffusion) nature of this quantity.
Note that in general the situation will actually be different to that illustrated above as the frequencies of the light pulses falling on the two detectors are not identical and thus the total energy that needs to be transferred is different for both, by an amount which may exceed <|Δε|>(θ) (let alone <Δε> ) by several orders of magnitude.
Even for parallel polarizers, a coincidence is therefore only possible after several 'passes' through the whole energy ranges h.ν1 and h.ν2 until in both channels an electron emerges simultaneously. This means that unless the ratios N1=h.ν1/Δε1 and N2=h.ν2/Δε2 divide by accident into some common smaller multiple, it takes N1.N2 light pulses until a coincidence occurs (this could by the way explain the circumstance that even for correlated atomic emissions (like in the Bell test experiments), the coincidence rate is usually several orders of magnitudes smaller than the individual count rates).
Basically, the same argument can also be applied to the correlated components of the energy increase (i.e. the first term in Eq.(7)) in case the electric field strengths and/or coherence times in the two channels are intrinsically different. Although the overall energy drift due to this term is dependent on the polarizer angle θ, the width of the individual energy steps depends on it in exactly the same way, i.e. a reduction of the coincidences in the above sense due to larger steps (and thus a total larger energy drift) is exactly offset by the fact that the acceptable energy 'bandwidth' for a coincidence to occur has now increased as well.
Old Version