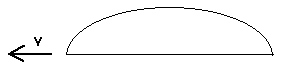
 Fig.1
Fig.1
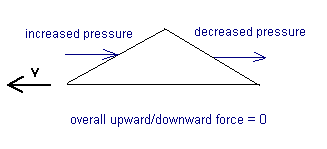 Fig.2
Fig.2
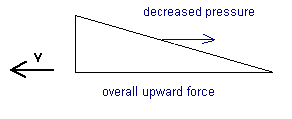 Fig.3
Fig.3
On the other hand, the reverse situation (Fig.4) should lead to a downward force, although Bernoulli's Law would again predict a lift.
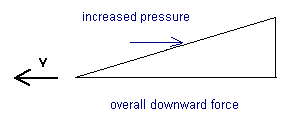 Fig.4
Fig.4
In this way one has also to interpret the frequently given example of blowing over a piece of paper. In fact, if one puts a sheet of paper flat on a table, fixes it to the edge of the table and blows over it from the edge, the paper will not lift by one millimeter, despite the motion of the air which according to Bernoulli's law should cause an underpressure.
The apparent attraction that is observed when blowing between two sheets of paper can be either explained by the fact that the sheets are in fact not exactly parallel to the airflow but bend away from it (hence reducing the pressure on the surface), or by the circumstance that the airflow does not cover the whole width of the paper (which leads to the stationary molecules being pulled into the airstream by means of friction (viscosity), which again reduces the pressure because molecules are removed from between the sheets; one can verify this by just using two narrow (1cm wide) strips of paper; these show no attraction but tend to stay parallel).
Either of these two mechanism should indeed be responsible for many of the phenomena attributed to Bernoulli's Principle. It should therefore be obvious that Bernoulli's law is only a viable physical explanation in cases where the viscosity of the medium is instrumental for the considered effect. Contrary to some scientific misconceptions, this is neither the case for the aerodynamic lift associated with airplanes nor for the drag of objects moving through a medium (see my separate page regarding aerodynamic drag and lift for a more detailed theoretical analysis of these issues). Note 1: it is frequently claimed by other critics of Bernoulli's law in this context, that Newton's law of action and reaction in connection with the observed 'downwash' of air near the wing is the explanation for the lift force acting on an airplane (see Ref. 1, Ref. 2). This view has to be rejected as well: this is not a problem of an action at a distance, but the only way a force can be exerted on a wing is by an increase of the number and speed of air molecules hitting the wing surface. Everything else, including the 'downwash', is merely a consequence of this, not the cause (some people argue that this cause/effect issue would be merely a semantic problem, but a) it is worrying if physicists don't care any more about the correct chain of cause and effect and b) the above examples show clearly that this can indeed be of practical relevance). Note 2: In contrast to the usual aerodynamic lift, the well known Magnus effect due to the rotation of objects does however not exist in an inviscid gas and can only be explained in terms of Bernoulli's principle:
consider a rotating ball that is moving through an inviscid gas (i.e. molecules interacting with the ball but not with each other): if the surface of the ball would be mathematically smooth, then the rotation would actually be without any effect at all because the air molecules would just bounce off like for a non-rotating sphere, but even for a realistic rough surface (obviously a surface can not be smoother than about 1 atomic radius), the overall effect still cancels to zero: the pressure on the side rotating against the airstream is higher at the front but smaller at the back (and the other way around for the co-rotating side) so overall there is no resultant force on the ball but merely a torque that slows down the rotation.
Hydrodynamics arguments (i.e. Bernoulli's principle) are therefore required to explain the Magnus effect but not for the aerodynamic lift.