Frictionless Buoyancy Acceleration If one has an object with mass m fully submerged in a medium (fluid or gas) in hydrostatic equilibrium in a gravitational field, it will, apart from the gravitational force
(1) Fg = m.g
experience the buoyancy force(2) Fb = - md.g ,
where md is the mass of the fluid (gas) displaced by the volume of the object (Archimedes' Principle).The total force on the object is therefore
(3) F = Fg+Fb = (m - md).g .
Normally, one would calculate the acceleration associated with Eq.(3) via Newton's first law as (see for instance Alonso, Physics)(4) a = F/m = g .(m - md)/m .
However, this is not correct because it does not take into account that the force not only accelerates the object but also the displaced fluid element (which has to fill the space vacated by the object).This is indicated schematically in Fig. 1.
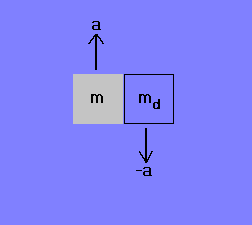 Fig.1
Fig.1
The acceleration of the object is consequently given by
(5) a = F/(m + md) = g .(m - md)/(m + md) .
This obviously makes much more sense than Eq.(4) as the maximum acceleration of the object is g (if the mass m=0) (from Eq.(4) one would derive an infinite acceleration in this case, but this is obviously not possible because the maximum acceleration for the displaced fluid is the free fall acceleration g). It is clear from the above consideration that buoyancy always leads to a net downward acceleration of mass, because even if the buoyant object rises, a greater mass of displaced fluid drops at the same time. This leads to an apparent weight reduction of the total system(6) ΔF = -(m - md).a = -g .(m - md)2/(m + md) .
It is obvious that without taking the displaced fluid element into account in the above sense, energy would not be conserved during the buoyant motion of an object as it would gain both gravitational potential energy and kinetic energy when rising in the fluid (thanks to Christopher for addressing the issue of energy conservation in this context (which led me to look into buoyancy more closely and formulate the above theory) and also for his experimental work which indeed confirmed the weight reduction effect (Eq.(6))).
Buoyancy Including Drag The above consideration holds obviously only for the idealized case with no friction. In reality friction will limit its applicability to very small velocities, which in practice may be exceeded already after a fraction of a second. The correct equstion of motion must then include the friction (drag) force
(7) FD = - 0.5.ρ.v2.CD.A
where ρ is the density of the fluid, v the velocity of the object, A its cross section area in a plane perpendicular to the motion, and CD the drag coefficient of the object (which is usually determined by experiment and typically has a value between 0.1-2 depending on the shape of the object).Instead of Eq.(3), the force equation must then be written as (taking Eq.(6) into account)
(8) F = (m + md).a = (m + md).dv(t)/dt =
= Fg +Fb +FD = (m - md).g - 0.5.ρ.v2(t).CD.A.
(9) v(t) = vT.tanh[g.(m - md)/(m + md) .t/ vT]
with the terminal velocity(10) vT = √ {g.(md-m)/0.5/ρ/CD/A}
(note that the sign of the argument under the square root has to be changed if the object is denser than the medium (m>md)).Eqs.(9) and (10) constitute the general solution for the velocity of an object in a buoyant medium. I have plotted the curve as a function of time for the case of a buoyant object in the gravitational field of the earth (g=981 cm/sec2 with cross section of A=1 cm2, mass m=0.5g, density of the medium ρ=1g/cm3 (water) i.e. md=1g, and a drag coefficient CD=0.47 (sphere).
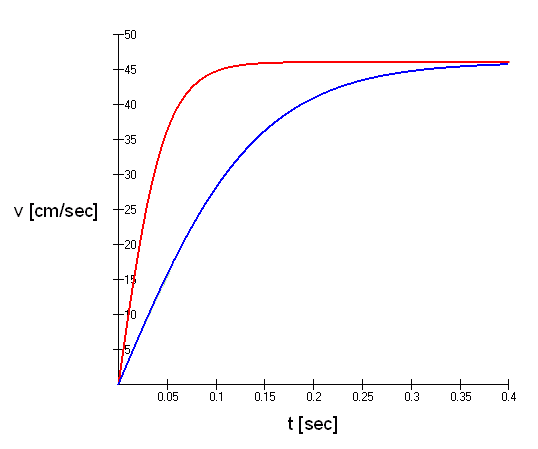 Fig.2
Fig.2
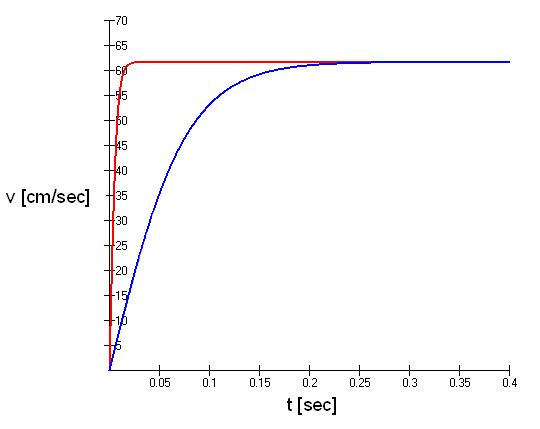 Fig.3
Fig.3