At the heart of Einstein's derivation of the 'Lorentz transformation' lies obviously the speed of light postulate, which he formulates in the introduction of his seminal 1905 paper as follows: light is always propagated in empty space with a definite velocity c which is independent of the state of motion of the emitting body. Let's apply this postulate to the following scenario as schematically illustrated in the below graphic: we have two detectors D, one at rest with regard to the light source (blue), and another moving with velocity v (red). Both are at a distance x from the light source L when the latter emits a light flash into their direction.
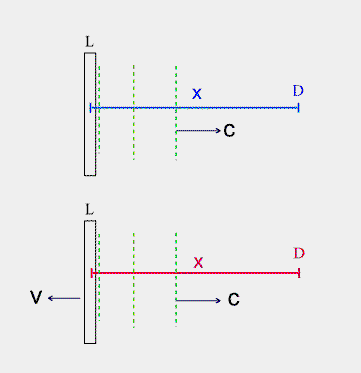
Applying the speed of light postulate to this scenario obviously implies that both the blue and red detector register the light flash at the same time
(1) tB =tR =x/c .
(assuming physically identical clocks).We can ask now whether this fact is not only a necessary criterion for the frame invariance of the speed of light here, but also a sufficient one.
Case A: Eq.(1) is also a sufficient condition:
In this case, the speed of light in either frame is fully defined by the detection event at the corresponding detector only (the detection event associated with the blue detector defines the speed of light in the blue frame, the detection event associated with the red detector defines the speed of light in the red frame). Defining the speed of light in the red frame by considering the detection events in the blue frame (as Einstein implies with his stationary frame timings x/(c-v) and x/(c+v)) is then not permissible.
Case B: Eq.(1) is not a sufficient condition:
We have to assume this if we want to define the speed of light in the red frame through the detection events in the blue frame (i.e. if we want the coordinate-transformed detector responses obey the speed of light postulate as well). The following animated graphic illustrates this point: assuming an array of detectors (rather than just one) for each reference frame, the top half shows the detector responses to the light flash for detectors of the corresponding reference frame only (case A above), the bottom half according to Einstein's definition of the speed of light in the red frame trough the blue detector events,
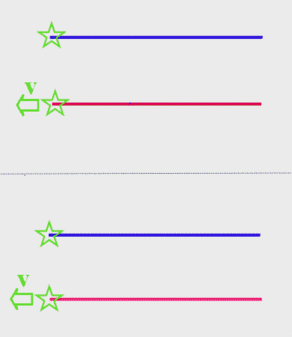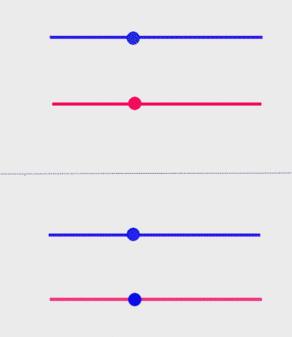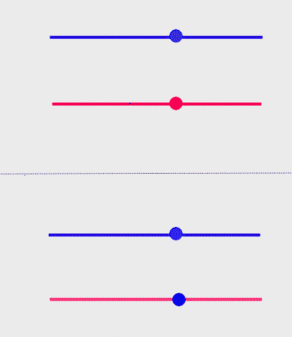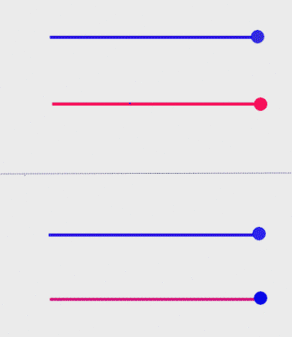
According to the speed of light postulate (Eq(1)) the x-coordinates of the detection events in the blue and red frames progress according to
(2) xB = c .tB
(3) xR = c .tR
where we have formally allowed different time units in both frames here. Of course, use of the same numerical value for the speed of light c here implies that x and t are proportional to each other, i.e.(4) xB/xR = tB/tR = a
Since the value of 'a' is just a matter of convention, we can, without loss of generality, choose a=1 and thus set(5) tB = tR = t
which gives us then(6) xB = c .t
(7) xR = c .t
Eqs.(6) and (7) are essentially illustrated in the top half of the animated graphics above.Now Einstein's interpretation of the invariamce of c implies that the transformed location of xB coincides with the location of xR in the red frame (as illustrated in the animation). In other words, we must have the identy
(8) xB' = xR = c .t = xB
where we used Eqs.(6) amd (7).This means that if we require that the transformed coordinate of xB moves also with speed c in the red frame (which is what Einstein assumes), this must be the identity transformation. So there can not be any velocity dependent transformation of the form
(9) xB' = γ.( xB -v.t )
Eq.(9) would only be consistent with the requirement Eq.(8) if v=0 and γ=1 (note that Eq.(8) requires that xB' changes sign when xB changes sign). This obviously contradicts the assumption that both reference frames are moving with regard to each other.Alternative Proof
We do actually not have to take any conventions at all about the time units used in the two reference frames but just note that the detection events associated with Eqs.(2) and (3) are completely independent of each other (the data in one frame can be obtained without having any knowledge of those obtained in the other frame). This system of equations consists thus of two independent variables (the locations of the detectors xB and xR) and two dependent variables (the corresponding detection times tB and tR). If we would require that the event (xR,tR) can be represented as a coordinate transformation of the event (xB,tB), we would have the additional constraints(10) xR = xB' = f(xB,tB,v)
(11) tR = tB' = g(xB,tB,v)
where f and g are the transformation functions of the arguments.However, (10) would turn the independent variable xR into a dependent variable, and (11) would , via the inversion of the equation, turn the independent variable tR into a dependent variable. There would thus be no independent variable left in the system of equations (2) and (3). This would be unacceptable both mathematically and physically.
Discussion
As is evident from both of the above arguments, any velocity dependent transformation is inconsistent with the speed of light postulate, Such a transformation is only applicable for material (massive) objects, for which the speed is not invariant in different reference frames. For those, independent measurements in the two reference frames (moving with velocity v relatively to each other) would instead of (6) and (7) yield(12) xB = u .t
(13) xR = (u-v) .t
i.e.(14) xR = xB -v .t
and thus a transformation equation of the form (9) follows naturally.In case of a propagating light signal, the problem is of course not the equation (9) but (8) where xB' is assumed to be co-located with xR. If we don't make this assumption, we can without any issues take for instance
(15) xB' = xB -v .t
as the speed of light postulate is independently satisfied by (6) and (7).And this would of course also remove the impossible situation of having a system of equations without any independent variables (as argued in version 2 above).
A re-evaluation of the special theory of relativity and/or its foundational postulates appears therefore to be advised.