The Special Theory of Relativity (as developed by Einstein) obtains a set of equations (i.e. the Lorentz Transformation formulae) which relates length and time units of two systems moving uniformly relatively to each other. Unlike the equations of the usual Galilei Transformation, these are not merely a linear transformation (describing the change in distance between two points due to the motion), but they are non-linear in the velocity due to an additional factor γ containing the ratio of the velocity and the speed of light (see for instance my
Aberration page for details). This factor γ corresponds to the amount of 'length contraction' and 'time dilation' that, according to Special Relativity, should be taken into account if transforming length and time units between different reference frames moving relatively to each other with non-zero velocity. However, this re-scaling of the space and time coordinates is in fact the result of Einstein ignoring the principle of the constancy of the speed of light by applying the usual vectorial velocity addition and then subsequently trying to compensate for this error by making a further error and changing the given length and time definitions (see my page regarding the
Speed of Light). As indicated on my page, with a consistent definition for the 'Speed of Light', no re-scaling of the length and time units is indeed required to make it independent of the motion of objects. The conclusions of time dilation and length contraction are hence invalid because they are based on a set of equations that is inconsistent with physical principles. This inconsistency is also evident from the well known 'Twin Paradox' which is due to the fact that motion is always only relative and any time dilation effect would therefore be ambiguous. Relativists claim that the situation would in practice never be symmetric as one observer has to turn around (and change the reference frame in the process) in order to compare the clocks (see for instance
http://www.phys.vt.edu/~jhs/faq/twins.html), but it is clear that this argument does not hold water as the time dilation should already be apparent before one observer turns around. This is best illustrated by the following thought experiment which does not involve any change of the state of motion of both observers:
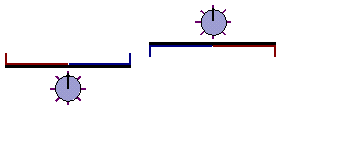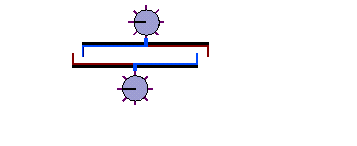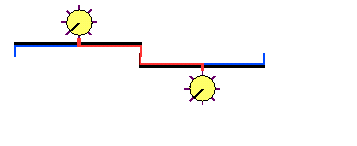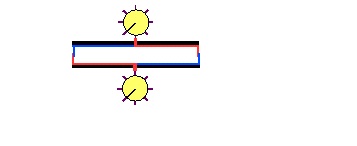
The following animation (kindly provided by
Corry Shores) may further illustrate the thought experiment:
One should note that the situation depicted above does not even involve any transmission of light signals at all and hence the basic assumption of Special Relativity does not apply in the first place. The clocks are started and stopped in each reference frame simultaneously (by definition, the contact starts each clock from zero) and both clocks will thus show identical times (for identical rods and clocks) after having been stopped (and after the clocks have been stopped, it is obviously irrelevant if A or B (or both) turn around to compare the clocks).
It should also be pointed out that the signal propagation time from the trigger points to the clocks is actually irrelevant here (whatever way of transmitting the signal is used): if the corresponding distances are identical in both systems, then the delay times will also be identical and there won't be any difference in the clock readings afterwards; if the distances are different, this would only result in a constant offset of the clocks which would be known and could be taken into account accordingly.
Note added: whilst it is clear that for the situation considered here the final clock readings must be identical (as it otherwise would lead to a logical paradox), some people claim that Relativity would actually not theoretically predict different clock readings in this case either, only if the situation is indeed asymmetric. It is then often claimed that the 'relativity of simultaneity' is responsible for the asymmetry i.e. the term vv.x/c2 in the Lorentz transformation formula t'=γ(t-v.x/c2). However, this is a false claim as the coordinate x=vt (for uniform motion) and therefore t'= t/γ (as is seen easily by inserting γ= 1/√[1-(v/c)2]). In §4 of his paper On the Electrodynamics of Moving Bodies, Einstein actually derives the same expression for the alleged transformation of the clock readings, which evidently depends only on the absolute value of the speed and neither on its direction nor the x-coordinate (i.e. it does not depend on the 'relativity of simultaneity'). Even if the velocity reverses at some point, this has no impact on the clock reading as t' depends only on v2 (by re-defining the origin x=0 as the reversal point for the 'return-leg' the same expression t'= t/γ does indeed apply to the outward and return legs). So even such an alleged 'asymmetrical' situation is in fact symmetric if the Lorentz transformation is applied correctly. In other words, the claim of time dilation shows in itself that that Relativity is an internally inconsistent theory.
As indicated on my pages relativity.htm, dynamics.htm and on the Relativity Forum pages, any alleged experimental evidence for the time dilation must therefore be due to actual physical effects (e.g. charged particles moving in electric and magnetic fields).