I. Introduction
Although expressions for the velocity and acceleration dependence of electromagnetic forces and the concept of retarded interactions were already developed by Gauss, Riemann, Weber, Lorenz and Maxwell in the early to mid 19th century, the notion of retarded potentials only came into general use after Hertz's experiments on electromagnetic waves and the discovery of the electron by Thomson towards the end of the century. This laid the basis for a kinematic consideration of the motion of charged particles and the resulting retarded potentials and fields. In this respect, Liénard and Wiechert were the first who, independently of each other, obtained the retarded electric and magnetic potentials of a moving point charge (which are consequently named Liénard-Wiechert potentials). Their solution, which is the basis of the corresponding derivations in all textbooks about electrodynamics (e.g. Jackson, Griffiths or Feynman), involves a spatial integration over the retarded density distribution i.e. a distribution which has undergone a scale transformation (being expanded or compressed compared to the unretarded distribution). However, all these derivations imply that the density is unaffected by this scale transformation, which means the transformed density distribution is not normalized anymore (or in terms of the physical interpretation here, the total charge is not conserved). Whilst this lack of normalization for the retarded distribution is acknowledged in some textbooks, it is seen as a natural mathematical consequence of the scale transformation caused by the retardation. However, this argument ignores the additional constraint imposed by the fact that a simple spatial re-organization of a system of particles must leave their total number unchanged. In this sense, section II of the present paper first formally examines the behaviour of density distribution functions under arbitrary (but particle-conserving) spatial transformation in general and linear scale transformations in particular. On this basis, section III formulates then the expression for the scalar potential associated with a spatially transformed density distribution in general and applies this result to the case of a moving point charge. In section IV (with the detailed derivation in Appendix A.1) the correct expression for the electric field of a moving point charge is derived from the so obtained scalar and vector potential. The result not only differs from the usual expression found in the literature because of the normalization issue mentioned above, but also due to a further mathematical mistake in the in the derivation of the Liénard-Wiechert fields when calculating the contribution of the acceleration term in the vector potential.II. Normalization of Density Distribution Functions
The concept of density distribution functions is a very important one in theoretical physics, as it enables the calculation of certain macroscopic physical quantities of many-particle systems in a closed way (something that would be difficult or impossible by considering individual particle kinematics). The density distribution function is therefore nothing more than a probability distribution function and as such is subject to certain constraints set by the physical state of the system (only by applying these constraints can an actually discrete distribution legitimately by approximated by a continuous mathematical function0. In particular is it required that the integral of the volume density distribution function over space must yield the total number of particles, and furthermore that this number is independent of time if the system is closed (that is. no particles are gained or lost), i.e.. for an ensemble of particles with the (average) volume density rho;(r,t) we have therefore the constraint(1) ∫ d3r ρ(r,t) = N
where N is the total number of particles, and the integration is performed over all R3 (or the volume elements for which rho;(r,t)>0 .We re-arrange now the spatial positions of the particles to yield a different distribution function ρ'(r,t) . Since no particles are gained or lost through a simple spatial redistribution, we must therefore also have
(2) ∫ d3r ρ'(r,t) = N
One can obviously relate the old and new distribution functions generally through(3) ρ'(r,t) = k(r'(r,t)).ρ(r'(r,t))
where r'(r,t) is an arbitrary transformation from the old particle coordinates (r,t) to the new coordinates (r',t) , and k(r'(r,t)) is a, as yet unknown, normalizating function which ensures (2) is fulfilled.,Inserting (3) into (2) yields then
(4) ∫ d3r k(r'(r,t)) .ρ(r'(r,t)) = N
and after changing the integration variable from r to r'(5) ∫ d3r' k(r'(r,t)) .ρ(r',t)/ λ(r'(r,t)) = N
where, according to fundamental calculus,(6) λ(r'(r,t)) = |det(∂r'/∂r)|
the absolute value of the determinant of the 'Jacobian' matrix(7) (∂r'/∂r) = ∂r'i/∂rj
of the first derivatives between the vector components of r and r'(r,t).From a comparison of (5) with (1) it follows thus
(8) k(r'(r,t)) = λ(r'(r,t))
(this is immediately evident if we take the integral in both equations to some upper limit and differentiate with regard to this limit) , so(9) ρ'(r,t) = λ(r'(r,t)) .ρ(r'(r,t))
For the special case of a simple scale transformation along, let's say, the x-axis, i.e. for(10) x'(x,t) = λ.x
where λ is some dimensionless scale factor, we have therefore(11) ρ'(x,t) = λ.ρ(λ.x,t))
In other words, distributing the same particles over a different scale changes the particle density accordingly, which is also intuitively obvious (note here that λ>1 reduces the scale of the spatial distribution and λ<1 expands it).In the next section we will apply this result to the case of the evaluation of the retarded potential of a system of moving charges.
III. Calculation of Retarded Potentials
For a stationary density distribution ρ(r), the electric potential at point is generally given by (using Gaussian cgs - units)(12) Φ(R) = q.∫ d3r ρ(r) / |R-r|
with q the individual particle charge (assumed to be identical here for all particles).If instead we have a time dependent distribution due to particle motion and assume a finite propagation speed of the potential, the total number of particles (and thus the total charge here) is preserved, but the instead of ρ(r) we have to integrate over a different distribution ρ'(r,t) that arises from the apparent time-layering due to the finite propagation speed, so with Eq.(9) we have (replacing the original position r in (12) with the retarded position r'(r,t))
(13) Φ(R) = q.∫ d3r λ(r'(r,t)) .ρ(r'(r,t)) / |R-r'(r,t)|
(in order to apply the concept of retarded positions , we have to assume here that r'(r,t) is a single-valued function, so effectively we have to consider the positions of individual particles).. Note that in (13) the density distribution is still formally written as a function of t (that is, unretarded in time), but it is a function relating to the retarded positions r'(r,t) . The latter are the only relevant aspect here for calculating the potential.
Changing the integration variable to r' analogously to (4),(5) gives then
(14) Φ(R) = q.∫ d3r' ρ(r'(r,t)) / |R-r'(r,t)|
Note that contrary to the usual derivation of the Liénard-Wiechert potential in the literature (as given originally by Liénard and Wiechert and repeated in many textbooks like those by Jackson, Griffiths or Feynman), there is no factor 1/λ(t) resulting from the variable change anymore, as it cancels out with the normalizing factor for the retarded density distribution (9). So there is in fact no direct dependence of the potential on the velocity v of the charged particles. The only difference of (15) to the stationary case (12) is that the density distribution ρ reflects the retarded positions r'(r,t) rather than the instantaneous positions r(t) . For instance, for a localized particle at the retarded position r'(r,t0) = 0 i.e. for a density distribution(15) ρ(r'(r,t0),t0) = δ3(r')
(14) becomes(16) Φ(R,t0) = q. / |R|
that is the same potential a charged particle at rest at the origin creates.In general, the potential depends obviously on the retarded positions r'(r,t) of all the charges. Once these have been determined (i.e. once the retarded distribution ρ(r'(r,t)) is known) the potential is derived in the same way as that of an identical static distribution. (i.e. as in (12)), although of course the retarded positions r'(r,t) depend in general on the observation point R , so they have to be re-evaluated for each R and t.
In order to illustrate the effect that the retardation has on the apparent charge density distribution and the resulting potential, we shall consider here a one dimensional scenario with a number of point charges at locations x within a finite length L and this whole configuration moving with speed v with regard to the observation point X (assumed >x) on the same line. The retardation condition in this case is
(17) X-x' = c.(t-t')
where x't' is the point and time of emission and X,t the point and time of detection. If we select the zero point of the time variable such that X=ct , the retardation condition is thus(18) x'=ct'
For the location of a uniformly moving charge, we have furthermore the constraint(19) x'=x+vt'
where x is the position of the charge at t'=0, from which we get immediately(20) x'=x/(1-v/c)
In Fig.1 below, this result is shown graphically for a number of charges between x=-L/2 and x=+L/2 , at the top for the charges at rest, and at the bottom according to (20) for the whole configuration moving with speed v=0.5.c towards the observation point .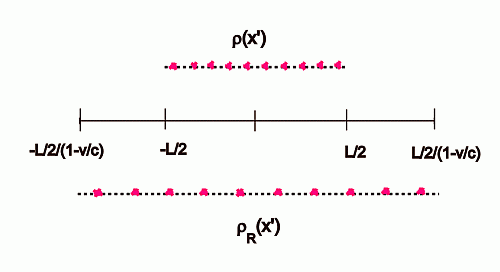
Fig.1: Retarded vs. unretarded density distribution
The expanded scale of the retarded distribution is due to the time layering of the picture caused by the different distances of the charges to the observation point X, which means that (assuming all charges are moving towards the observer) a signal from a distance closer than the origin has to be emitted at a later time t' in order to be observed at time t at point X, whereas a signal from a distance further than the origin has to be emitted at an earlier time. The retarded distribution is therefore spread over a corresponding range of retarded times. This of course is nothing new as such, and the derivation of the retarded potentials in the literature (following on from the work of Liénard and Wiechert) is indeed based on this circumstance, but it has been apparently overlooked that the expanded scale of the retarded distribution (by a factor 2 in this example) goes along with a corresponding decrease of its density, thus keeping the total charge constant, as already shown formally in Sect.II. Trying to keep the charge density in the bottom section in the diagram identical to that at the top whilst maintaining the expanded scale would be equivalent to doubling the number of charges for the retarded distribution (or alternatively doubling the value of the elementary unit charge). The Liénard-Wiechert potential, as derived in the literature throughout, is thus solely the result of a violation of charge conservation in this sense.
Of course, for a spatially expanded distribution as in this case, the apparent change of the spatial scale due to the retardation will result in a velocity dependent potential observed at a point X, but this velocity dependence disappears if the scale of the charge distribution becomes infinitesimally small. For instance, if we consider just the two outermost charges in Fig.1 i.e. if
(21) ρ(x) = δ(x-L/2) + δ(x+L/2)
and thus(22) ρ(x') = δ(x'-L/2/(1-v/c)) + δ(x'+L/2/(1-v/c))
so(23) Φ(X) = q.∫ d3x' ρ(x') / |X-x'| = q/[X-L/2/(1-v/c)] +q/[X+L/2/(1-v/c)]
If we let now L->0 (i.e. joining the two particles with charge q into one particle with charge 2q at the origin), we obtain(24) Φ(X) = 2q/X
that is the classic Coulomb potential of a charge 2q located at the origin, regardless of the speed of that charge with regard to the observer at X.IV. Electric Field of Moving Charge
Whilst potentials are a useful mathematical concept in physics in general, the observationally relevant quantity is only the associated field that causes the local action on any particles. On the basis of Maxwell's equations, the electric field is in this sense obtained from the equation (again in Gaussian cgs units).(25) E(R,t) = -∇Φ(R,t) - 1/c.∂A(R,t)/∂t
where, analogously to the scalar potential (15),(26) A(R) = q/c.∫ d3r' v(r'(r,t)).ρ(r'(r,t)) / |R-r'(r,t)|
is the vector potential created at point R, t due to motion of charges at their (retarded) positions r'(r,t) (as in the previous sections, all primed variables indicate here and in the following retarded quantities).If we want to calculate the field of an individual charge, we have to set the density distribution
(27) ρ(r'(r,t)) = δ3(r'-s(t'(t)))
where s(t'(t)) is the path vector of the particle at the retarded time t'(t). With this, the potential and vector potential become (from (15) and (26))(28) Φ(R,t) = q/ |d'(R,t)|
(29) A(R,t) = v(s(t'(t)))/c.q / |d'(R,t)|
where(30) d'(R,t) = R-s(t'(t))
It is straightforward to show (see Appendix A.1) that in this case(31) ∇Φ(R,t) = -q/λ(R,t) . d'(R,t)) / |d'(R,t))|3
and(32) 1/c.∂A(R,t)/∂t = q/c2 . [ a'/|d'(R,t)) + 1/λ(R,t) .v'v'.cos(θ)/ |d'(R,t))|2 ]
with(33) λ(R,t) = 1 - v'/c.cos(θ)
= where θ is the angle between the velocity vector v' and the relative vector d'(R,t) from the retarded position of the particle .to the observation point,Furthermore, a' = ∂v'/∂t' .
With (25), the electric field thus becomes
(34) E(R,t) = q/λ(R,t) . d'(R,t)) / |d'(R,t))|3 - q/c2/λ(R,t) .v'v'.cos(θ)/ |d'(R,t))|2 - q/c2.a'/|d'(R,t))
The first term in this expression is solely due to the potential gradient and constitutes a field vector pointing from the retarded position of the charge to the observation point, whereas the second and third terms are solely due to the induction term (32) and represent field vectors pointing anti-parallel to the retarded velocity and the retarded acceleration respectively. Both of the latter are only of second order (~v'2/c2 and ~a'/c2), with the velocity dependent term vanishing altogether if the velocity vector is normal to the position vector (cos(θ)=0).It is furthermore of crucial importance that the acceleration term does not contain the velocity dependent factor 1/λ(R,t) = 1/(1-u'.v'/c) . Otherwise, Gauss' law would not hold (see Appendix A.2). Nevertheless, in contrast to the usual result for the Liénard-Wiechert field (see Appendix A.3), the local radial flux due to the acceleration term does in fact not vanish identically here, but only as an average over the whole sphere.
One should also note that despite the factor 1/λ(R,t) in the first two terms in (34), neither the radial nor the transverse electric field at any point R diverges v' as approaches c, because by scalar multiplication with u' we obtain (ignoring the acceleration term)
(35) Er = E(R,t).u' = q/λ(R,t)/|d'(R,t))|2 - q.v'2 cos2(θ)/c2/λ(R,t)/ |d'(R,t))|2 =
= q/λ(R,t)/|d'(R,t))|2 .(1-v'2 cos2(θ)/c2) =
= q/|d'(R,t))|2 .(1+v'. cos(θ)/c)
(36) Et = |E(R,t)×u'| = q/|d'(R,t))|2 .v'2/c2.cos(θ).sin(θ)/(1 -v'/c.cos(θ))
This is in stark contrast to the fields obtained from the usual Liénard-Wiechert potentials (see Appendix A.3)V. Conclusions and Outlook
The present investigation has shown that the well known Liénard-Wiechert potentials in the theory of electrodynamics are based on unnormalized particle distribution functions and thus violate the law of charge conservation in case of moving charges. The correct expression for the scalar potential of a moving charge does not contain an explicitly velocity dependent factor but only the retarded instead of the instantaneous position. And the resulting electric field does consequently not show the same divergent behaviour for charges approaching the speed of light as the corresponding solutions based on the Liénard-Wiechert potential. It is beyond the scope of the present work to examine in detail the consequences of this fact for the theory of electrodynamics and beyond., but the implications should be of a fundamental nature for any problems involving relativistic kinematics of charged particles, be they of a theoretical or experimental nature.Appendix A1
Derivation of Electric Field Of Moving Charge
a) Field Due to Scalar Potential
The first contribution to the electric field comes from the gradient of the scalar potential (28)(A.1.1) ∇Φ(R,t) = ∇(q/ |d'(R,t)|)
With(A.1.2) d' = |d'(R,t)|)
we have thus (using the chain rule)(A.1.3) ∇Φ(R,t) = ∂Φ/∂d' .∇Rd' = -q/d'2 .∇Rd'
With the definitions(A.1.4) R = (X,Y,Z)
and(A.1.5) x'=X-s'x ; y'=Y-s'y ; z'=Z-s'z
we have (see (30))(A.1.6) d'(R,t) = (x',y',z')
and noting that(A.1.7) ∇R = (∂/∂X , ∂/∂Y , ∂/∂Z)
and(A.1.8) d' =√(x'2+y'2+z'2)
the x-component of ∇Rd' can be written as (using the chain rule)(A.1.9) ∂d'/∂X = 1/2d' .[ 2x'.(1-∂s'x/∂X) - 2y'.∂s'y/∂X - 2z'.∂s'z/∂X ]
Now because of the retardation condition(A.1.10) d' = c.(t-t')
(where t' is the time emission and t the time of detection), x, y' and z' are only implicitly functions of the detector coordinate X , so we have to apply the chain rule(A.1.11) ∂s'x/∂X = ∂s'x/∂t' .∂t'/∂X = -v'x/c .∂d'/∂X
(A.1.12) ∂s'y/∂X = ∂s'y/∂t' .∂t'/∂X = -v'y/c .∂d'/∂X
(A.1.13) ∂s'z/∂X = ∂s'z/∂t' .∂t'/∂X = -v'z/c .∂d'/∂X
where we have used the fact that ∂s'x/∂t', ∂s'z/∂t' and ∂s'z/∂t' are nothing but the components of the (retarded) velocity of the charged particle.After inserting (A.1.11)-(A.1.13) into (A.1.9) we obtain after a little algebra using the fact that (see (A.1.6))
(A.1.14) x'.v'x + y'.v'y + z'.v'z = d'.v'
(A.1.15) ∂d'/∂X = x'/d' + d'.v'/d'/c .∂d'/∂X
or(A.1.16) ∂d'/∂X = x'/d'/(1-u'.v'/c)
with(A.1.17) u'=d'/d'
the unit vector from the retarded position of the charge to the observation point.Analogously we get for the Y and Z components of the gradient of d'
(A.1.18) ∂d'/∂Y = y'/d'/(1-u'.v'/c)
(A.1.19) ∂d'/∂Z = z'/d'/(1-u'.v'/c)
and thus(A.1.20) ∇Rd' = u'/(1-u'.v'/c)
With this (A.1.3) becomes(A.1.21) ∇Φ(R,t) = -q/(1-u'.v'/c) .d'/d'3
a) Field Due to Vector Potential
According to Maxwell's equations, the second contribution to the electric field arises from the time derivative of the vector potential (see (25)). Since the vector and scalar potentials of single particle with (retarded) velocity v' are related by (see (28),(29))(A.1.22) A(R,t) = v'/c .Φ(R,t)
we have
(A.1.23) 1/c.∂A(R,t)/∂t = 1/c2 .∂(v'.Φ(R,t))/∂t =
= 1/c2 .[ Φ(R,t).∂v'/∂t + v'.∂Φ(R,t))/∂t ] =
= 1/c2 .[ 1/d'.∂v'/∂t + v'.1/d'2.∂d'/∂t ]
In the way of a total time derivative, the first term in the bracket describes the change of the vector potential due a change of the current (i.e. v') at constant distance (i.e. d'), whereas the second term describes the change of the vector potential due to a change of the distance of the current system at constant current.
Therefore, the derivative ∂v'/∂t in the bracket has to be taken at fixed d', which means the light travel time is fixed as well, so from (A.1.10) we can conclude that for this term any variation in the time of detection must equal the variation in the emission time i.e. ∂t'=∂t and thus
(A.1.24) ∂v'/∂t = ∂v'/∂t'
For the second term in the bracket in (A.1.23), the time derivative of d' is easily obtained from (A.1.8) using again the chain rule
(A.1.25) ∂d'/∂t = 1/2d' .[ -2x'.∂s'x/∂t) - 2y'.∂s'y/∂t - 2z'.∂s'z/∂t ] =
= 1/2d' .[ -2x'.∂s'x/∂t') - 2y'.∂s'y/∂t' - 2z'.∂s'z/∂t' ] .∂t'/∂t =
= -u'.v'.∂t'/∂t
(A.1.26) ∂t'/∂t = 1 -1/c.∂d'/∂t
so (A.1.25) becomes(A.1.27) ∂d'/∂t = -u'.v'/(1 -u'.v'/c)
Inserting (A.1.24) and (A.1.27) into (A.1.23) we have therefore (with a'=∂v'/∂t' )(A.1.28) 1/c.∂A(R,t)/∂t = q/c2 .[ a'/d' + v'.(u'.v')/(1 -u'.v'/c) ]
Appendix A2
Electric Flux for Moving Charges (Gauss' Law)
In order to check the consistency of the solution (34) for the electric field of a moving charge with Maxwell's equations, we first and foremost have to calculate whether the resultant flux through a closed surface complies with Gauss law(A.2.1) 1/4π.∫∫4πdS.n.E = q
where n is a unit vector normal to the surface element dS at that point. Since generally the surface element dS is related to the solid angle element dΩ over the radial distance R by(A.2.2) dS = R2.dΩ
we can rewrite (A.2.1) as(A.2.3) 1/4π.∫∫4πdΩ.R2.n.E = q
We can simplify the integral significantly by choosing, without loss of generality, a spherical surface and assuming the charge producing the electric field at the origin. In this case the retarded distance |d'(R,t)| in the expression for the electric field (34) has the same constant value R anywhere on the sphere, and by choosing the polar axis along the directions of d'(R,t) ,v' and a' respectively for the 3 terms in (34) we can restrict ourselves to the integration over the polar angle θ due to the azimuthal symmetry, i.e.(A.2.4) R2/2.0∫πdθ.sin(θ).[Fd'(θ)+Fv'(θ)+Fa'(θ)] = q
where(A.2.5) Fd'(θ) = q/R2/(1-v'.cos(θ)/c)
(A.2.6) Fv'(θ) = -q/R2 .v'2.cos2(θ)/c2 /(1-v'.cos(θ)/c)
(A.2.7) Fa'(θ) = -q/R .a'.cos(θ)/c2
Inserting these expressions into (A.2.4), it is immediately obvious that the acceleration term does not contribute anything to the total electric flux as the integral over sin(θ).cos(θ) from 0 to π is zero. For the sum of the other two terms we can write
(A.2.8) Fd'(θ)+Fv'(θ) = q/R2.(1-v'2.cos2(θ)/c2) /(1-v'.cos(θ)/c) =
= q/R2.(1+v'.cos(θ)/c)
Appendix A3
Electric Field for Unnormaized Distribution Function
As explained in Sects II and III, the usual derivation of the scalar an vector potentials (as found in the literature throughout, starting with Liénard and Wiechert) has an erroneous factor(A.3.1) 1/λ(R,t) = 1/(1 -u'.v'/c) = 1/(1-v'.cos(θ)/c)
that violates charge conservation as it makes the total charge aspect (i.e. position) dependent., so in this case the potentials are taken as(A.3.2) Φnn(R,t) = q/λ(R,t) .1/|d'(R,t)|
(A.3.3) Ann(R,t) = q/λ(R,t) .v'/c .1/|d'(R,t)|
where the subscript 'nn' shall indicate that the density distribution is not normalized i.e. violates charge conservation.We state here without going into the details of the calculation that in this case, following essentially the same procedure of calculating the spatial and time derivatives by applying the chain and product rules accordingly (only this time including the additional factor 1/λ(R,t) ), one obtains for the electric field
(A.3.4) Enn(R,t) = q/λ3(R,t) .1/|d'(R,t)|2 .[ (u'-v'/c).(1-v'2/c2+d'.a'/c2) - d'.a'/c2.(1-u'.v'/c) ]
This is the expression usually found in the literature i.e. also including the factor 1/λ(R,t) incorrectly applied to the acceleration terms when doing the derivatives of the product terms involving v' (as discussed in Appendix A.1.b).Even though (A.3.4) may be consistent with Gauss' law, this can at best be taken as an average statement regarding charge invariance, which however as such is only a necessary condition but by no means a sufficient one. And the erroneous factor 1/λ(R,t) in the usual Liénard-Wiechert potential simply invalidates the required independence of the total charge as a function of the aspect angle θ .
Apart from the incorrect additional factor 1/λ2(R,t) applied to the overall amplitude of the electric field, (A.3.4) also obtains a spurious linear 'aberration' term v'/c added to the location unit vector u' even if the induction terms (which only cause higher order corrections) are ignored. This is frequently interpreted in the literature to the effect that the retarded electric field points to the present positions of the particles rather than the retarded positions (see for instance Griffiths or Jackson), which is a logical contradiction in terms only caused by the erroneous derivation of the Liénard-Wiechert potentials (A.3.2) and (A.3.3) in the first place.
In contrast to the electric field obtained from the properly normalized charge distributions (see (35), (36)), the electric field based on the usual Liénard-Wiechert potentials shows a diverging behaviour as v' approaches c, as the radial field becomes (ignoring the acceleration terms, which vanish anyway)
(A.3.5) Enn,r = Enn(R,t).u' = q/λ3(R,t) .1/|d'(R,t)|2 .(1-v'.cos(θ)/c) .(1-v'2/c2) =
= q/|d'(R,t)|2 .(1-v'2/c2) /(1-v'.cos(θ)/c)2
For the transverse electric field (A.3.4) yields instead (again neglecting the acceleration terms)
(A.3.6) Enn,t = |Enn(R,t)×u'| = q/|d'(R,t)|2 .|v'.sin(θ)|/c .(1-v'2/c2) /(1-v'.cos(θ)/c)3