Time Dilation and Twin Paradox Debunked

The Special Theory of Relativity (as developed by Einstein) obtains a set of equations (i.e. the Lorentz Transformation formulae) which relates length and time units of two systems moving uniformly relatively to each other. Unlike the equations of the usual Galilei Transformation, these are not merely a linear transformation (describing the change in distance between two points due to the motion), but they are non-linear in the velocity due to an additional factor γ containing the ratio of the velocity and the speed of light (see for instance my Aberration page for details). This factor γ corresponds to the amount of 'length contraction' and 'time dilation' that, according to Special Relativity, should be taken into account if transforming length and time units between different reference frames moving relatively to each other with non-zero velocity. However, this re-scaling of the space and time coordinates is in fact the result of Einstein ignoring the principle of the constancy of the speed of light by applying the usual vectorial velocity addition and then subsequently trying to compensate for this error by making a further error and changing the given length and time definitions (see my page regarding the Speed of Light). As indicated on my page, with a consistent definition for the 'Speed of Light', no re-scaling of the length and time units is indeed required to make it independent of the motion of objects. The conclusions of time dilation and length contraction are hence invalid because they are based on a set of equations that is inconsistent with physical principles. This inconsistency is also evident from the well known 'Twin Paradox' which is due to the fact that motion is always only relative and any time dilation effect would therefore be ambiguous. Relativists claim that the situation would in practice never be symmetric as one observer has to turn around (and change the reference frame in the process) in order to compare the clocks (see for instance http://www.phys.vt.edu/~jhs/faq/twins.html), but it is clear that this argument does not hold water as the time dilation should already be apparent before one observer turns around (the difference in the final clock readings must have accumulated during the whole time considered).

I shall examine the inconsistencies and logical paradoxes implied by the Lorentz transformation in more detail below, first from a purely algebraic point of view, then for a couple of thought experiments supported by appropriate graphics.

Algebraic Time Dilation Paradox

The time dilation claim is based on the set of Lorentz transformation for the space and time coordinates relating the rest frame (unprimed coordinates) and moving frame (primed coordinates)

(1a) x'=γ(x - vt) ; (1b) t' = γ(t - vx/c²) .

In §4 of his paper On the Electrodynamics of Moving Bodies, Einstein derives the time dilation effect by considering the origin of the moving frame x'=0. Inserting thus (Eq.(1a)) x=vt into Eq.(1b) he obtains (considering that γ= 1/√[1-(v/c)²])

(2) t' = t/γ

. This would mean that the clock rates in the moving (primed) frame would be a factor 1/γ slower than in the rest frame (time dilation). However, according to the principle of relativity, the choice of the rest frame is obviously arbitrary, so with the same right the primed system can consider itself at rest. Using the inverse Lorentz transformation

(3a) x=γ(x' + vt') ; (3b) t = γ(t' + vx'/c²) .

. and applying, analogously to above, the condition x=0 i.e. x'=-vt' (from Eq.(3a)) one obtains now

(4) t = t'/γ,

which is obviously an algebraic contradiction to Eq.(2), that is a 'twin paradox' arises from the alleged time dilation effect (a corresponding inconsistency is also apparent for the length contraction, as is immediately evident by comparing Eqs.(1a) and (3) for t'=0 and t=0 respectively). These inconsistencies are simply the consequence of the Lorentz transformation having been derived through inconsistent assumptions and mathematics in the first place.

Twin Parodox Thought Experiment

The following thought experiment gives a further proof that the Lorentz transformation is logically inconsistent and leads to completely different conclusions regarding the interpretation of events in different reference frames, not only with regard to the timeline of the events, but, due the physical interaction of the two systems, with regard to the whole causal chain of events.
Consider two space ships A and B that have an encounter at a relativistic velocity v. The proper length of each ship is L, so the other space ship will appear length contracted to L/γ. I have depicted 3 instances of the encounter sequence in each of the ships' reference frame A and B (with the corresponding rest ship shown as the solid line, the moving ship as the dashed-dotted line. The (irreversible) flow of the ship times t_A and t_B is from top to bottom. The zero point of the time scale (i.e. t_A=t_B=0) is chosen to correspond to the moment when the left sides A1 and B1 of both ships match up with each other (middle frame). Now assume that at an earlier time t_A=t_B =-L/v*(1-1/γ), when the right sides of the ships match up in frame A, there is an explosion that will affect (or even destroy) both ships (triggered for instance by contact pins on each ship at A2 and B2). However, in frame B, due to the inverse Lorentz contraction, A2 and B2 have not met up yet, so no explosion is possible as yet. Even in the second frame (t_A=t_B =0), A2 and B2 have not matched up yet in frame B (whereas in frame A both ships are already damaged for a while). And if at this moment the contact mechanism is disabled in ship B, there won't be any explosion at all in frame B even if A2 and B2 eventually match up at t_A=t_B = L/v*(1-1/γ) (last frame). So whilst in frame A both ships are now largely destroyed, in frame B they still are moving along as if nothing had happened, i.e. we have a twin paradox (note that in this case the twin paradox solely appears to be due to the different length contractions rather than any time dilation).

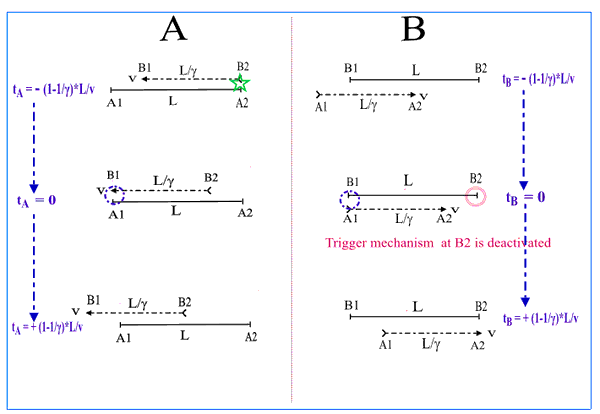
Time Dilation/Length contraction experiment where the Twin Paradox could not be resolved without violating causality

It is clear from this twin paradox thought experiment that the Lorentz transformation merely suitably offsets the events in time so that the effect of the Lorentz contraction of the moving reference frame is being compensated for. Relativists usually get away with this because they assume physically unconnected events.Any possible interaction between the two systems however result in causality issues (like in this case). And the point is that any kind of clock or length comparison will always require some kind of interaction between the frames (otherwise the issue would be a purely academic one).
It is evident from this thought experiment that the Lorentz transformation can not preserve the physical intergrity of a macroscopic physical object. If one has a spaceship, or any other physical object, then the physical reality of everything that goes on within it can not possibly depend on some observer, in particular not its relative motion. The only thing that would be observer dependent is the relative velocity of the spaceship, but nothing to do with the internal physical composition. And the latter is exactly what the Lorentz tranaformation implies as it simply transforms different parts of the spaceship to different times (i.e. different instances of existence). This is physically not possible. One can not transform a single atom of an object to a different time without compromising its whole existence.

Again, these paradoxical results are simply the consequence of the Lorentz transformation (including the implied effects of time dilation and length contraction) having been derived through inconsistent assumptions and mathematics in the first place.
And as indicated on my pages relativity.htm, dynamics.htm and on the Relativity Forum pages, any alleged experimental evidence for the time dilation (and length contraction) must therefore be due to actual physical effects (e.g. charged particles moving in electric and magnetic fields).

Note: this page is a complete re-write of the orginal version, discussing a different (and, as I think, more convincing) scenario for the twin paradox. Click here for the old version (to which for instance some comments on my discussion pages are relating).