Comment by Chris Stevenson (Physics of Clouds)
It is well known that clouds are a mixture of water vapor and small condensed water droplets. It is claimed in texts relating to cloud formation that, even though they are heavier than air, these small droplets do not fall to the ground because of upward convection currents. I flatly do not believe this. I must confess to being an engineer, not a physicist, so can offer no detailed alternative explanation, but I have an inner conviction that the true explanation may be that there is an attractive-repulsive equilibrium between the water vapor and the interspersed droplets, which allows the cloud to float at a height consistent with its net density. I am aware that many cloud density measurements have been made which no doubt refute my claim. Could these be in error for some reason ? When flying in aircraft, one often finds oneself between two distinct layers of cloud, and according to conventional wisdom one is expected to believe that convection is occurring between these layers. I don't.
Reply
First of all, Cloud Physics is indeed a theory with several unknowns and speculative assumptions. However, it seems inevitable to me that there is always some kind of convection associated with clouds. This is because the cloud scatters most of the sun's radiation back into space and the base of the cloud is therefore almost completely shadowed. This results in a substantial temperature decrease at the base of the cloud both compared to the top of the cloud and the ground, and hence causes a convection both within and below the cloud (the latter is for instance utilized by gliders to gain height; when it is generally overcast, the temperature at the ground is of course as much reduced as at the base of the cloud and no convection should develop here (which may be the reason why gliders only tend to fly when the weather is fine)).
However, convection is hardly the explanation why water droplets with less than a certain weight do not fall to the ground. The point is that the speed with which the droplets fall is proportional to their radius and small droplets fall so slowly, even in stationary air, that they evaporate before they reach the ground (I made a rough calculation according to which a droplet with a radius of 1mm falls with a speed of 3m/sec, but a 1μm droplet falls with only 3mm/sec). Having said this, it is of course well possible that water drops become charged due to mutual collisions, which means their fall would be affected by electric fields (which are for instance assumed to be present in thunderstorm clouds).
I think the above aspects are largely acknowledged by present Cloud Physics (although not fully understood in detail). It is the general nature of clouds which is in my opinion misrepresented (or not addressed at all) in the corresponding literature: clouds are not necessarily volumes of higher water vapor concentration in the air, but, almost paradoxically, indicate volumes with fewer (albeit larger) droplets than the surrounding region. The amount of water in a given volume element being equal, only those regions will scatter light (i.e. appear as clouds) where the distance between two droplets is more than the wavelength of light. This is a general phenomenon in optics according to which the assumption of 'individual scatterers' breaks down if this condition is not met and instead the assumption of a 'continuous medium' has to be applied, in which case the scattering is confined to the forward direction i.e. there is no scattering at all (which is for instance why one can see through water). As droplets tend to attach to each other at smaller relative speeds, larger droplets (and hence smaller droplet numbers) will preferably form at lower temperatures. This is in my opinion the condition for water vapour to appear as clouds (or fog at ground level), but not the presence of certain 'condensation nuclei' (dust etc.) that are presently assumed to be required for the development of rain drops.
Comment by Chris Stevenson (Theory of Elasticity)
It is often claimed at the beginning of texts on the theory of elasticity, which is based on the generalized Hookes Law, that the concept of stress can tell us what the internal forces are at points within in a body. But this not true in either a practical sense or a philosophical one. From the practical perspective, if we apply a uniaxial stress to a body, it shrinks in a transverse direction. But a simple application of the theory of elasticity reveals that there is no stress in that transverse direction, either direct or shear. Any theory that purported to tell us something about the internal forces in a body would surely need to reflect the fact that the atoms in the transverse direction had become closer to one another, and that forces in that direction had increased. Very well, you may argue, but the theory of elasticity is a holistic one, and assumes that matter is an endlessly divisible continuum, not a collection of atoms. But on this basis also, the concept of force at a point is meaningless, since we define stress at a point as the limiting value of the stress experienced by the faces of an infinitesimal cube encompassing the point, as it shrinks in size. But then the limiting values of the forces and areas are both zero, so the force at such a point can have little meaning. In the last analysis, the theory of elasticity is precisely what its title says - it tells us how things deflect when stresses are applied, and not much more in any absolute sense.
Reply
Hooke's law is generally used as a macroscopic relationship like the laws of Optics and Thermodynamics. Unlike the latter two however, it is in principle also assumed to be valid for individual molecules (
see reference). The macroscopic object is therefore basically assumed to behave according to this force between two atoms in a molecular bond. Obviously, the size of molecules represents the lower limit for the application of Hooke's law and the Theory of Elasticity.
However, in my opinion there appears to be an inconsistency with this interpretation of elasticity. From the width and height of the potential curve given in the above reference, one would have to conclude that one should be able to roughly double the distance between the nuclei before dissociation occurs. However most elastic materials like metals can only be stretched by up to 1% before they fracture, so this would mean that the distance between the nuclei in the material can only increase by 1% as well before dissociation occurs. This however would require a potential curve with only about 1% the height and width as the one shown. Obviously, a crystal lattice is somewhat different from irregular molecular associations, but I don't know any quantitative argument which would explain this discrepancy (I searched the web and also posted the problem in some physics forums, but did not get any answers so far).
This raises the question if Hooke's law is probably instead associated with the shear stress on folded molecule chains (which would also answer your first point regards the transverse stress). If you consider the following schematic arrangement of rigid sections connected by joints:
It is obvious that if you pull the chain apart longitudinally, it will contract contract in the transverse direction (which is what one observes if one stretches a rubber band for instance). The transverse stress is here simply a result of the shear angle of the rigid sections. It is reasonable to assume that this type of expansion will also follow Hooke's law, but it will obviously reach the limit if the sections are all in one line. Maybe metals and other harder materials have more or less the molecules lined up already and can therefore only expand by a very small amount. This still does not give a criterion for the breaking point of the chain however.
Chris Stevenson (2)
I was not really trying to find fault with the theory of elasticity, which of course can never apply exactly to any real material and really belongs ultimately to the field of mathematics. I was only pointing out the philosophical difficulty in giving physical meaning to holistic concepts like stress and pressure.
One of the first to study the relationship between atomic structure and the theory of elasticity was Poisson, who assumed only central forces between atoms and concluded that every material should have a Poisson's ratio of .25, which of course is not true - there are even materials with negative Poisson's ratios. In arriving at this conclusion, he considered a solid as being made up of atoms arranged something like Fig. 39-10 in Volume 2 of Feynman's lectures on Physics. My only point is that the Sodium and Chlorine atoms in this diagram will become closer in a transverse direction when an axial (top to bottom) force is applied, even though there is no stress in this direction - so in trying to make simple analogies about internal forces from a theory about stresses, one will be easily misled.
Towards the end of your reply , you state "The transverse stress here is ............". But there is no transverse (orthogonal) stress in this situation according to the theory of elasticity. The maximum shear stress is at forty five degrees to the line of action of the applied force.
Regarding breaking strain, it should theoretically lie somewhere between 10 and 20 % for all materials, which is obviously not true. As far as I am aware, the much lower strength of real materials is today well understood, and is explained by Griffiths cracks and dislocations.
Reply (2)
As macroscopic objects consist of a huge number of atoms, one has to introduce holistic concepts like density, pressure, temperature etc. in order to be able to describe their properties quantitatively at all (one should be aware however that this is only an approximation which may not be applicable in all circumstances). The problem is how to interpret these macroscopic properties in terms of atomic physics: for instance, the electrostatic force between two charges decreases with distance ~ 1/r
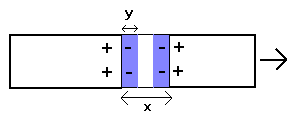
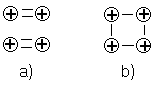
2, yet the stress force for a macroscopic object increases proportional with its extension (Hooke's law). The latter can therefore only be explained by a collective particle behaviour (Hookes law applies for instance also in plasma physics if one considers collective displacements of the electrons from the ions (plasma oscillations)). Within certain limits, the individual molecular bond apparently also exhibits such a 'harmonic oscillator' behaviour, but as indicated above it is much too strong (by about a factor 100 at least) to account for the observed stress fracture point of materials. However, for larger aggregates of atoms (e.g. crystal lattices) the bond should in principle be much weaker, as the electrons are shared by more atoms. As illustrated below, if one has for instance four nuclei forming two individual molecules, there are two electrons forming the bond for each molecule (a), but there is only one molecule forming the bonds if all nuclei are arranged in a single aggregate (b)
Unfortunately, I could not find any information how this affects the bond in crystal lattices (apparently, it is generally assumed it doesn't), but in my opinion the consequences should be substantial for many materials (the molecular bond is usually relatively weak compared to the electrostatic energies of the individual particles and may not even survive removing half the number of bond electrons). Although a weaker molecular bond would explain the observed breaking stress of materials, it would obviously not account for the elastic behaviour as given by Young's modulus and Hooke's law. This suggests that the latter might in fact be caused by a different force, and, as already indicated above, it could be related to plasma polarization fields caused by stretching the material: if the positive charges in the material are displaced by a distance x due to an applied force, free electrons will move into the space created and thus create a polarization field (displacement field) which pulls the positive charges back (as illustrated below)
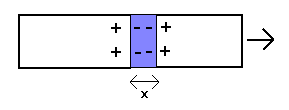
The stress (force per unit area) associated with this is given by the equation
S = 4π.n.e2.x .n2/3 = 4π.n5/3.e2.x ,
where n is the free electron density, e the elementary charge and x the displacement.
Now, Hooke's law holds typically only for a relative strain of less than 0.3% (see Fig.3 in
Reference) which requires a stress of the order of S=10
9dyn/cm
2 (i.e. a weight of 1000 kg/cm
2). Assuming the average distance between the nuclei in the material to be 10
-8cm, their corresponding displacement is therefore x=3
.10
-11cm. Inserting these values into the above equation, one finds that the free electron density in the material is n=2
.10
22 cm
-3 (i.e.about 3% of the atom density).
With this interpretation, the maximum possible displacement y of the plasma electrons should depend on their kinetic energy K through the equation
K = 2π.n.e2.y2 .
For thermal electrons of room temperature (300
o K), one finds a value of about y=10
-9cm, i.e. Hooke's law would hold up to a relative strain of 10%, in contradiction to experiments. The discrepancy could be explained by the neglection of elastic collisions of the plasma electrons which will reduce the displacement to the average collision length
y = 1/(n.σc) ,
where σ
c is the Coulomb collision cross section which for room temperature (300
oK) has a value of about 10
-11cm
2. This yields now a value of 2y=10
-11cm, in good order of magnitude agreement with the observed elastic limit of x=3
.10
-11cm. For a larger strain than this, the plasma polarization field will fail to bridge the gap between the two sections and the corresponding force will vanish, as schematically depicted below:
In this region (i.e. beyond point 3 in Fig.3 in the above 'Reference' link) the molecular bond (in its reduced strength as explained above) might then be responsible for the stress vs. strain curve.
Stress inhomogeneities in the material should be important as far as the spatial location of the breaking point is concerned, but I don't think it explains the relatively small stress needed for fracture. I had a look at the Griffith's theory of cracks yet could not find a quantitative answer in this respect either. The theory seems to be able to describe how cracks evolve under stress but not how they develop in the first place. In fact, the crack interpretation suffers from a crucial logical flaw: in order to explain the unexpectedly small work required to homogeneously stretch the material to the yield point, the molecular bonding energy would have to be reduced by the cracks to less than 1% of the theoretical value from the outset (i.e. even without any stress applied), which is absolutely inconceivable.
If you are applying an axial stress force on an object, it is of course only the geometrical arrangement of the atoms in the lattice which can lead to an internal shear stress and a transverse stress component as a result. The point is that generally the situation is symmetrical (stress will occur in opposite transverse directions), so you may feel you are only applying an axial force. But nevertheless, some of the work you are doing will go into the transverse rather than the longitudinal strain.
Comment by Vlad Tarko
You describe the ambiguity in the definition of the
Lorentz force, but you exaggerate the ambiguity and don't explain it properly.
You ask relative to what is the velocity that appears in the definition of the Lorentz force. The point that one needs to make is that this ambiguity is closely connected to the ambiguity surrounding the magnetic field. There aren't two different ambiguities. In fact, the magnetic field doesn't really exist, it is always possible to choose a certain frame of reference R where the magnetic field is zero (only electric field exists). Magnetic field appears because we don't always use such a frame of reference (due to practical reasons). The velocity in the definition of the Lorentz force is relative to this frame of reference R (I hope I'm not mistaken about this, I haven't really checked the mathematical details involved here).
This point is highly relevant because electromagnetism agrees with the principle of relativity precisely because magnetic fields don't really exist. The principle of relativity holds because all fundamental forces are velocity independent (and thus one can measure velocity only by using its definition, and thus only relative velocities exist). If magnetic fields would exist in all frames of references, Lorentz force would depend on velocity and thus the principle of relativity would crumble (one could use magnetic phenomena to measure absolute velocity).
The magnetic field is a pseudo-field similar (although a little bit different) to the pseudo-forces that appear when one describes motion relative to a non-inertial frame of references (like the centrifugal force).
Reply
I don't think that I exaggerate the ambiguity with the definition of the Lorentz force:
if you consider a current in a wire, then this current (and hence the associated magnetic field), is independent of the reference frame as it is in fact given by the sum of the currents of the positive and negative charges in the wire and thus depends only on the relative velocity of the two but not on the velocity of the test charge (the velocity appearing in the Lorentz force). In this case there is therefore no frame where the magnetic field is zero for the test charge (as in fact it is the same in all reference frames). The question therefore remains relative to what the velocity v in the Lorentz force has to be measured. It is obvious that this has to be a physical definition and the only thing that makes sense in my opinion is the center of mass of the current system producing the magnetic field (which in the case of the wire would be practically the frame where the wire (i.e. its positive charges) is at rest).
It should be quite obvious from this consideration that you run into ambiguities with regard to the definition of the Lorentz force unless the electric current (and thus the magnetic field) is frame-independent, and the only way to achieve this is by having actually two different types of charge carriers (i.e. electrons and ions) moving relatively to each other. However in order to be more than just the superposition of two different currents (which would inherently not change anything about the existence of the ambiguity), this has to involve a physical interaction of the two kinds of charges. Collisions between charged particles are in my likely to be the actual cause for magnetic field generation (for an anisotropic particle flow, the contributions from the individual collisions will not cancel each other and an overall magnetic field results).
Vlad Tarko (2)
This is incorrect. The current is the amount of charge that passes through a surface S in a unit of time. If this surface moves alongside the wire in such a way that the average charge that passes thru it is zero, the current (relative to the frame of reference of this particular surface) is zero. The value of the current is NOT independent of the reference frame. The magnetic field in this particular reference frame is also zero. Consequently, in this reference frame, the Lorentz force acting upon any test charge will be only the electric force. Describing the motion of the test charge relative to such a reference frame may not be very practical but, at least in principle, it can be done.
If one moves the surface S one gets not only an electronic current but also a current caused by the ions of the metal crystal - that now are passing through surface S. In order to have a total zero current the ionic current through S must be equal to the electronic current thru S. So, the surface S doesn't move with the same velocity as the free electrons, but with half that velocity.
Reply (2)
I am afraid your picture of the situation is still incorrect:
consider first the wire in a reference frame where the ions of the metal lattice are at rest and the electrons are moving with a velocity u. The current in this frame is -A
.n
.e
.u (where A is the cross section of the wire, n the density of the free electrons and e the elementary charge). As the ions are resting in this reference frame their contribution to the current is zero.
Now consider the total current in a reference frame moving with velocity v relative to the ion lattice: the current due to the electrons is -A
.n
.e
.(u-v) and the current due to the ions is -A
.n
.e
.v, that is the total current is again -A
.n
.e
.(u-v) - A
.n
.e
.v = -A
.n
.e
.u , i.e. it is independent of the velocity v of the reference frame (it only depends on the relative drift velocity u of the electrons and ions in the wire). Since the total current is independent of the reference frame, so is therefore also the magnetic field of the wire. This leaves the Lorentz force law ambiguous unless one refers the velocity v to a physically preferred reference frame (which obviously must be somehow related to the current system producing the magnetic field i.e. the wire in this case).
P.S.: As you were apparently referring to the relativistic interpretation of the Lorentz force above (according to to which the magnetic force should vanish in a reference frame comoving with the particle and be replaced by a corresponding electrostatic force), I have debunked this view now on my page regarding
Magnetic Fields and Lorentz Force. Anyway, it should be clear that the magnetic field
B of a wire can never be zero as the current which produces is given by the difference of the currents of the positive and negative charges and is thus independent of the reference frame. On the other hand, you will run into ambiguities with the definition of the magnetic force if the current consists only of one kind of charges as both the current (and thus
B) as well as the velocity
v would become frame dependent (the Lorentz force would be zero in the reference frame where the current is zero as well as in the frame where
v is zero). Thus one can conclude that a magnetic field can actually only be created by two physically interacting currents of charges.
Comment by Roberto Ponzi
I'd like to receive your comments about the following problem of the Faraday Law of classical electromagnetics.
The Faraday Law states that the line integral of the electric field around a closed curve is equal to the rate of change of the magnetic flux through a surface that has that curve as border. This law may be experimentally valid for small systems but if we consider a larger system we find some impossible predictions. For example consider a large circular ring, made of conducting wire, and a magnetic source at the center of the ring. The Faraday Law predicts that the electric field inside the wire will change at the exact time of change of the magnetic source, which is impossible in reality because there must be a delay between the change of the magnetic source at the center of the ring and the appearance of the electric field on the border of the ring. In other words the Faraday Law is non-local and requires instantaneous effects. Of course for small distances the delay is very small and it isn't noticed, but the law is itself flawed.
This is only one of the many flaws of the standard Maxwell equations that are taught in schools today.
Reply
I agree that Faraday's law is strictly speaking flawed (as a fundamental physical law at least) but not for the reason you are giving:
first of all, Maxwell's equations in their differential form are obviously local, but according to accepted theory, the right hand sides of the equations are strictly speaking retarded values (see for instance
this link) (in the integral form, the retardation is actually often explicitly written). However, it is exactly this retardation which I consider as theoretically flawed as it leads to inconsistencies with the concept of a static force (which would become dependent on the reference frame; see my page
The Inconsistency of the Retarded Field Concept for Static Forces for more). There is in fact no causality problem with an instantaneous interaction; causality would only be violated if the effect comes
before the cause.
However, as indicated on my home page entry regarding
Maxwell's Equations, causality (or at least locality) is in fact violated by the appearance of a time derivative in the induction equations (the definition of a derivative always requires two function values, so the problem can not be local in time (as the form of the equations pretends). This suggests that Faraday's law is actually not a fundamental law but only an approximate macroscopic consequence of the Lorentz force.
Roberto Ponzi (2)
I've also read the discussion about the magnetic field and the Lorentz force and I am concluding that the problem is if the magnetic field is really caused by just charges in relative motion respect to the detector or not. An electric current inside a conductor wire is not a simple flow of negative charges, maybe the following experiment could show the truth:
Let's take a thin insulating wire, made of plastic or glass, and shape it into a circular ring. Let's put on it an amount of electrical charge by adding or removing electrons, spread the charge uniformly over the ring to have a uniform linear charge density "l". Then let's spin the ring around its axis at high speed.
According to the standard theory this should be equivalent to a loop of current made with a conductive wire.
It is easy to find that the current intensity is given by Q*f where Q is the total charge of the ring, given by 2*pi*R*l, and f is the rotation frequency (number of turns per seconds). If the spinning ring was equivalent to the loop of current we would have a magnetic field at the center of the ring, directed along the ring axis, and with intensity B = mu_0 * I / (2 * R).
This experiment is very basic, has it ever been performed ? Maybe it can be a bit difficult to achieve a quantity of charge Q large enough, but we can compensate by increasing the rotation speed. With today's magnetic field sensors it should be possible to measure very low magnetic fields around the spinning ring.
The importance of such tests is enormous as the relativists have build their castles just on the problems of classical electromagnetics.
Reply (2)
I don't know whether such an experiment has been performed or whether it could be technically performed (note also that one might have to do this in a vacuum in order to prevent the air from getting involved in this), but logically it shouldn't produce a magnetic field, because (as pointed out on my home page entry regarding
Maxwell's equations) the magnetic field would then be observer dependent (e.g. a co-rotating observer would see no magnetic field) and the Lorentz force q/c
.vxB would thus, contrary to experience, become a quadratic function of v, as B would be proportional to v as well. So as it is clear that B has to be independent of the observer, it can only be determined by a net relative motion of two kinds of charges in their mutual electric fields (which obviously is the case if one has a current flowing in a conductor).
You have to remember that Maxwell's equations have only been conceived on the basis of experiments in electrical engineering, i.e using currents in wires, and everything else is just a mathematical abstraction (which is indeed inconsistent in case of the induction laws, even though in an engineering sense (i.e. macroscopically) it may be a good approximation).
Note that the relativistic theory of the magnetic field is in any case inconsistent, as it not only suffers also from the flaw that the Lorentz force would be frame dependent, but it would also lead to inconsistencies with Maxwell's equations (i.e. the Biot-Savart law) (see my page
Magnetic Fields and Lorentz Force for more).
Comment by Robert Miller
I stumbled across the web page
Bernoulli's Principle and Airplane Aerodynamics and I have some issues with the analysis.
If your analysis in Fig 1 and 2 were correct, then, as a race car driver, it would not be such a challenge to generate down force on the front of the vehicle. Any race car driver can tell you first hand how at high speeds the front end tends to lift. For a dramatic example, see the dramatic blow over incidents of the
Mercedes CLK at Le Mans (eg ) and this with a car specifically designed to aerodynamically generate down force. The point here is that yes, a torques will be created as you described in your figures, but this is an independent action and force and that the airflow also creates lift - forces are additive, not exclusionary. The result being that "lift" IS generated irrespective of any rotational force, and if the rotation if canceled such as by rigidly applying a counter torque (eg elevator control on an aircraft) the net result will be lift. Also, as a pilot, in point of fact a real aircraft wing uses both Bernoulli AND impact airflow to generate lift. The airfoil of an aircraft wing is canted so as to create an incident impact airflow to the underside of the wing. Thus total lift is a result of both the Bernoulli velocity (a function of air craft speed) and the impact lift on the underside of the wing (a function modulated by the incident angle by use of the elevator control). Thus for level flight at varying speeds, generation of lift is apportioned between Bernoulli and impact by use of elevator control.
You also incorrectly refer to an experiment of blowing over a sheet of paper. The flaw here is that it is a separate pressurized air mass flowing over the top than below. That is, the air mass over the top is of a different pressure as a result of it's being compressed and expelled across the top independent of the air mass below that is at ambient pressure. And yes. if you blow it at an angle to the paper, the impact force will overwhelm any lift that would be generated if the air mas pressure was not increased to produce the airflow in the first place. The fact that there is no net lift produced is not proof that no lift was created. Forces add, and the impact force could simply have been greater than the lift force.
You also state that an air mass in motion parallel to a surface cannot exert a force on that surface. Really? Air is a compressible fluid and exists at some pressure. This means that an air mass will exert an expansive force in all directions in response to that pressure (basic heat energy thermal properties of molecules in motion in gases). Thus a net relative motion parallel to a surface does not negate the motion of the gas molecules "outward" in all directions and thus there will be a motion component that IS normal to the surface which thus creates a force normal to that surface. The net macroscopic parallel airflow velocity does not negate the molecular Brownian motion, which cannot be ignored in any compressible liquid. And this is the genesis of Bernoulli's principle. The air mass over the top of the "wing" is at lower pressure due to its velocity and thus it's pressure force normal to the surface as a result of that pressure is less than the pressure force normal to the bottom surface. And since forces add, there is a net upward force that is the difference between the two - this is lift.
Also, if Bernoulli is a myth, how do you explain the operation of the basic carburetor?
Fundamentally I think you are analyzing the wrong phenomena. Bernoulli has to do with pressure forces resulting from pressure differentials between air masses in relative motion. What you are discussing is the velocity impact forces of air molecules. These are two distinctly different phenomena.
Reply
I appreciate your comments, but I don't quite understand why you think they would invalidate my analysis regarding the
Aerodynamic Lift. First of all, as a general note, if a racing car turns into a (badly behaved) airplane, it is hardly a testimonial for the correctness of the standard theory of aerodynamics. Secondly, if you watch the video, then they even mention that the accident happened because air got
underneath the car, lifting the front up as a result and flipping it over. Ideally this should of course not happen on a straight and smooth surface, but in reality the underside of the car will not always be parallel to the track surface (probably also due to air turbulence), and if the front only slightly lifts up, the air stream will lift it up even further and eventually flip it over. If the same scenario is applied to my Figs. 1 and 2, exactly the same thing would happen. The point is that my figures assume ideally a zero angle of attack, and thus no such lift should occur, only the torque due to the airstream potentially pushing the front down and lifting the back up.
From this it is also obvious that an airstream fully parallel to a surface will not exert any force on the latter. As I mentioned on my web page, it will only exert a force if the air streams only past a part of the surface. In this case the viscosity if the air (i.e. the friction due to mutual collisions of air molecules) will pulls stationary molecules from outside the airstream into the latter, hence reducing the pressure over the surface. This effect also essentially explains the carburetor (Venturi) effect. You can call this the Bernoulli effect if you like, but, contrary to the usual theoretical claim, it is solely due to the
viscosity of the air and would not occur in an inviscid fluid (unlike the aerodynamic lift, which indeed is essentially only due to the impact of the air molecules).
Question by Kenny Danielson
Airfoil lift by Bernoulli doesn’t seem correct to me either, but then there is this simple, often repeated demonstration. Hold a sheet of paper vertically. Grasp the sheet by the bottom edge and it will fall away taking the shape of an airfoil. Now blow across the top of the 'airfoil' and watch it rise.
How is this explained?
Reply
I mentioned the 'paper sheet' example already on my page
Bernoulli's Principle and Airplane Aerodynamics . The lift here is caused by the fact that due to the curvature of the sheet you are blowing away from its surface. This will pull the stationary air away from the sheet and thus cause an under-pressure (which lifts the back of the paper up). If the airstream is fully parallel to the paper surface it does not work at all (just put a piece of paper flat on a table and blow carefully parallel over it (better tape the paper to the edge of the table so that you can't blow underneath); the sheet will not lift by one millimeter in this case).
As explained on my page, this is different from the aerodynamic lift as it works only because of the viscosity of the air (i.e. the mutual collisions of the air molecules). Airplanes in contrast would in principle also fly if the air would be completely inviscid.
See also the previous entry on this discussion page.