I read your dismissal of L.'s postulation that gravitational field might define the speed of light. I don't think your dismissal holds water.
1. According to S.Hawking, the 'spacetime' bend had to be taken into account for GPS units, otherwise they would have been out hundreds of miles. I am quite certain that deep space orientation is made by on board computations, and not by earthbound observances.
2. All mass is connected by gravity. This means that we and the distant stars are connected by gravity. Where would you suspect would be the "points in space where the gravitational field is zero."?
3. By my theory, gravitational links create the carrier field for light wave propagation, and it is therefore necessary that gravity affects the massless wave which follows it.
Reply
L.'s comment was referring to the Michelson-Morley experiment. It was his suggestion that, despite its negative outcome, one can maintain the concept of an 'ether' (with regard to which light travels with speed c), if one assumes it to be fixed to the local gravitational field (i.e. the rest frame of the mass producing this field). The problem is however that the gravitational field can only be defined through the gravitational force which in turn depends only on the distance to a mass but not its velocity. Furthermore, it is impossible to tell just from the local gravitational force alone how many masses at what distances actually contribute (superposition principle).
It is therefore very much implausible (and in fact impossible without a new physical concept) that a light signal actually 'knows' the exact positions and velocities of all the masses in the universe that contribute to the local gravitational field, in particular if this happens to be zero because all the gravitational forces cancel by accident. As outlined in my reply to L., a 'gravitation-bound' propagation speed c should have been observed already for instance when communicating with interplanetary space craft because c would have to be referred to the gravitational field of the sun rather than that of the earth (which means the travel time of the signal would be misjudged by about 1 sec, making exact maneuvering next to impossible).
As far as I am aware, radar tracking of space probes from earth is the only way to determine their distance (through the travel time of the signal) and its velocity (through the Doppler shift). By means of comparing the observations from different radar stations (the 'Deep Space Network'), one can then also calculate the exact direction i.e. its actual location in 3D-space. But all this depends obviously very much on the assumptions one makes regards the propagation of the radar signal. With regard to your argument that the curvature of space-time should make a significant difference for the communication with interplanetary space craft: as outlined in the Gravitational Lensing - entry on the main page, it is very much implausible that massless entities like electromagnetic waves should in any way be affected by gravitation. Corresponding observations could well be explained by electromagnetic phenomena.
In any case, this should be insignificant here: starlight bent in the gravitational field of the sun is delayed by about 10-6 sec (corresponding to a distance of the order of 100 meters) and the delay in interplanetary space will be even less than 1/100 of this because of the smaller gravitational field (despite the larger distances). This would therefore certainly be negligible for any practical application. A.M.(2)
Your suggestion that a 1 second delay would be noticed makes me ask, have you ever noticed the 3 second delay of a transatlantic telecommunication ?
Anyway, I fail to see how you, of all people, could make the argument that this couldn't be, because someone would have noticed.
"Gravitational field can only be defined through the gravitational force which in turn depends only on the distance to a mass but not its velocity." What makes you say this? Our lack of understanding of the gravitational field does not presuppose that velocity does not affect it. If light is an actual wave, it must have a carrier. The only field which we know of which connect ourselves to the mass of distant stars is gravity. If light is carried on gravity, then C is primarily an attribute of gravity. The effect which slows down the moving clocks must be affected by some field, in order to slow it down. As it seems to be heading towards an 'all stop' at C, this field has the same attributes of the light carrier and thereby shows evidence of being the light carrier. If it is not a gravitational effect, what could it be? Reply(2)
You are arguing from the naive viewpoint of high-school physics, i.e. with regard to waves on a water surface, sound waves etc.. These kind of waves waves are obviously only disturbances of the medium through which they propagate and have no existence of their own. A light wave on the other hand is an entity that carries itself (strictly speaking, according to Maxwell's equations, the electric component of an electromagnetic wave carries the magnetic component and vice versa).
Anyway, what kind of scientific logic are you applying here ? My theoretical arguments above besides, all experiments so far have clearly indicated that there is no carrier medium for light waves (which have to be referred to the source and receiver alone), so why do you take this as a support for your assumption that gravitation is the carrier medium ?
I feel I can accept the notion that time is a perceptive effect "stuff" when experiencing the passage of "Events". However, if C is invariant, the reduction of distance between moving bodies will produce light wavetrains that will out-run earlier produced wavetrains and in effect create reverse time in action and there would be a breakdown in Chronology. You could watch a clock (pulsar) run backwards!
Reply
The apparent (observed) sequence of events is always different from the actual sequence if the propagation speed of the signal is finite and the distance between source and observer changes due to motion (see for instance my discussion with M.P.). The speed of light was actually derived by Römer in 1676 in this way by comparing the apparent change of the orbital period of Jupiter's moons due to the motion of the Earth. However, this is basically the case whether or not the propagation speed is invariant (the latter would only give a correction to this) and holds therefore also for sound waves and many other phenomena. If the speed of the motion exceeds the propagation speed of the signal, then the event would indeed appear to run reversely in time, but you could not say that time itself would run backwards or chronology as such would break down (if a gun is fired 1 mile away and one second later another gun is fired right next to you, then you will here the latter first and the former only 4 seconds later although it was fired earlier; you certainly would not want to claim here that time is running backwards as it is just the consequence of the different distances of the two guns and the finite sound speed).
Any remote event can therefore only be used as a chronological standard if you know exactly the relative motion of source and observer and any other physical processes affecting the travel time of the signal. Only then is it possible to make conclusions about the actual chronology of the event. Simon Pennington (2)
That would imply that there is a genuine chronology viewpoint that exsists outside of reality somewhere?.. remember I am talking about a single body problem and light. The two gun example is true for exploding stars whatever... but from one moment to the next for an accelerating body the image front it projects down the axis of motion would create problems unless C is independent and invariant? You are saying even if you observed this you could not know anyway? Reply (2)
A chronology can only be defined through physical events, so it would be wrong (or at least useless) to say that a genuine chronology exists outside reality. The problem is to make sure that the physical system defining it is simple enough so that it can serve as a standard, i.e. other physical events can be easily compared to it without making too many transformations. As you are not omniscient however, you can strictly speaking never be sure if you took all possibilities into account which could affect the apparent chronology. With regard to the motion problem, you could observe the system from different positions and/or over an extended period of time, but a) this may be impractical in practice and b) you may still have neglected other physical effects. Science in general can just only serve as an approximation of reality, but you can never really know if your assumptions apply in each and every individual case.
As mentioned already, the invariance of c has nothing to do with the chronology problem (it does not cause it nor does it remove it). A chronology can be defined without involving light at all, although if you use light, the invariance of c (which is a consequence of the wave nature of light) should be correctly taken into account if you want to have an accurate chronology (see my page regards the Speed of Light for this). Simon Pennington (3)
You seem to say we just do not know and/or this has not been addressed. Chronology as defined seperate from light needs to use transformations of some sort to define each "event"? The resort to definition via simplicity is a contradiction with any idea that chronology exists at all. An indefinable system of definitions places great strain on the concept in the first place..I take your point about scientific models but would add I have yet to have any 2 sources agree in any way on this question. Reply (3)
As indicated before, the chronology of any event, whether communicated by light or other means, will be distorted by a number of factors that need to be corrected for if you want to make any objective statements about the event. The reduction (transformation) from the subjective to the objective (independent of the observer) viewpoint is one of the fundamental principles of physics and does not put any more strain on the concept of chronology than on any other physical principle (the fact that the size of an object is apparently smaller when observed from a distance does not question the concept of size either unless you believe that the object actually gets smaller). Only Relativity claims that chronology and size do not exist in an objective sense, but this is due to a wrong interpretation of the speed of light and the assumption that a chronology and length can only be defined by light signals.
A typical thought experiment used to explain time dilation and length contraction uses the two postulates of relativity, two observers, A and B, and a light clock, which is a light source and a vertical rod with a mirror attached at each end.
The two observers are in (inertial) motion, and each observer is unaware of his own (inertial) motion. Observer A is the one with the light clock. So while the two observers are in motion relative to each other, observer A and the light clock are stationary relative to each other, and observer B and the light clock are in motion relative to each other.
Usually, (in the typical thought experiment for time dilation and length contraction) a diagonal line is drawn, connecting the flashes of light.
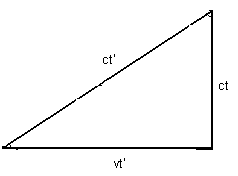
Then the Pythagorean theorem is applied, and from there the time dilation equation is derived.
However, to correctly apply the Pythagorean theorem all three side of the right triangle must represent the same type of measurement. Since the two sides each represent a vector velocity while the hypotenuse is not a vector velocity, we do not have a right triangle for which all three sides represent the same type of measure. The gamma factor is the quantity used as the time dilation factor in relativity theory. The problem with it is that the hypotenuse of the right triangle is used as a vector velocity (which, of course, it is not), and the Pythagorean theorem is applied (which, of course, it should not be). The consequence is that there is no actual time dilation or length contraction.
Note: this is an edited version of an article published in full under http://www.wbabin.net/taylor/svotph.htm.
Reply
This is essentially the point I made elsewhere on this site: it is an incorrect conclusion to assume that your diagram describes the propagation of the light signal for observer B. It is in fact the lightpath for observer A projected into system B under the assumption that a vectorial velocity addition applies to light. In reality (because of the invariance of c) , the light signal also has to travel vertically for observer B. However, Einstein mistakenly applied the vector addition as shown above (which he should not have done), and since this obviously would result in a non-constant speed of light, he redefined his spatial and temporal measuring units (which he should not have done either). He apparently did not realize that two wrongs don't make a right. The solution to the problem is that it is the concept of 'speed' which has to be redefined for light (see my page lightspeed.htm), not the measuring units of time and space (it is anyhow preposterous to assume that the rate of clocks or the length of rods should in any way be determined by the propagation of light signals; obviously, time and space units can be defined without any reference to light at all).
Simon Aldred
I'm not convinced by the argument for time dilation, but in your reply to this comment you say that the light beam, according to observer B, must travel vertically and that vector addition is wrong. Will the light still hit the top mirror in B's frame of reference as the mirror is moving from left to right according to B? In A's frame the light hits the mirror and in B's it doesn't. This seems contradictory if we're trying to describe the same event!
Reply
It only seems contradictory because you are applying the usual concept of speed which implies a frame dependence. However, the speed of light is supposed to be strictly invariant and independent of any motion, so both detectors should register the flash exactly vertically here (in their respective frame). The two detectors will of course be in different locations when they register the flash, so the point is that there is no such thing as a unique event in the case of light signals. Each event only makes sense if referred to the frame of the corresponding detector. If there would be an 'aberration' from the vertical direction, then the speed of light would not be invariant anymore (in view of the observed aberration of starlight, this raises in my opinion the question whether the speed of light is indeed only invariant with regard to a longitudinal motion but not with regard to a transverse motion).
I would like to say a few words about basic, fundamental , time, mostly because when I look for a formal definition of time, all I can find is nothing more than references to various periodic motions which can be used to measure time, and the practical benefits of everybody referencing the same time system rather than their ad hocing it locally. I feel a little more needs to be said about time than just that. It appears to me that when we measure time all we are doing is comparing the progress of one motion with another reference motion (or identical copies of it). We usually pick a periodic motion, of some sort, for the reference motion because it automatically sets up its own units for counting, but I think most of us tend to forget what it is we are counting, namely the total number of units of periodic motion the periodic motioner is doing compared to the other motion (activity) we are evaluating. I feel this forgetfulness tends to give time the apparent abstract character of an independent existence which would remain in space after all matter were, somehow, removed. In other words,if one were all alone in definitely empty space one could still count to one's self. But, of course, this would still be a motion of some sort in one's head.
Also, some people postulate the possibility of traveling in time (not just figuratively). We can initiate travel in space, but since time is, apparently, just measured amounts of motion, and motion maintains itself (does its own thing), it seems to me that all we can do about motion is just stand by and watch, and also try to redirect some of this self asserting motion towards our own beneficial uses. Having described what I think time is I would like to mention a couple of complications we run into when logging the times of events. First of all, if observers are scattered around at many different locations they will record different views of the environment for any given point in their chosen common time system. If they are far enough apart for the delay in the arrival of light to be significant in there counting of time they will also record slightly different starting times for any events in their ranges of view.
What about the effect of the propagation delay of light on the appearance of any simultaneity of events? It is obvious that all observers anywhere on a line equidistant from two events will all agree about the apparent relative simultaneity of those two events.
On the other hand, all those observers who are not on a line equidistant from the two considered events will disagree with all those observers who are on the equidistant line, about any appearance of simultaneity. The same goes for any observers who move off the equidistant line during the time of light travel from the two events. This latter hypothetical situation has been erroneously used by some authors, including Einstein, as a basis to claim that a different time rate frame necessarily exists for moving observers, or bodies. A different time frame does necessarily exist for moving bodies, but not because of any altered evaluation of relative simultaneity, because this also can happen with non moving bodies. Rather is the fact of a different time rate frame for moving bodies on account of some basic dynamics of physics uncovered by Maxwell and Lorentz, and subsequently verified by others.
All the above observers can, of course, reconcile their disagreements by calculating out the delays in the arrival time of light to their locations from the particular events, and arrive at a common "real time" log of the events, providing nobody is moving fast enough to cause the Special Theory of Relativity to become a significant factor. If the Special Theory of relativity becomes a factor then alternate time rate frames are set up which can also be calculated out using the Loran Transformation, but it is currently considered to be against the rules to call either one of the time rate frames the only real one. They are both said to be real. However, since most of the matter in the universe, at least "close by", is in the same time rate frame, I see no reason why we couldn't refer to a "Common Relative Time" and an "Extrinsic Relative Time", the latter phrase being applicable to more than one possible time rate frame of course. In this way fictitious (or real) super speed space travelers could be hooked into a common time system by using the Lorentz transformation, and agreeing to accept "Common Relative Time" as the basic, common, reference time.
Reply
First of all, it is worth noting that the definition of time has never been an issue in physics before Einstein came along and confused people's minds with his metaphysical (and logically inconsistent) relativistic concepts of time and space (see my Relativity Page). As you correctly indicate, potential practical problems with the definition of time arise only if this involves propagating signals of some sort. However, as pointed out by me in my discussion above with Simon Pennington, this problem exists independently of the invariance of the propagation speed, i.e. it is not limited to light signals. For light signals, the fundamental difference lies with the definition of 'speed' not with the definition of 'time' (see my page regarding the speed of light).
With interest and appreciation I discovered your site. I have a remark about aberration. To my regret I don't have time to develop this fully, but perhaps the following suffices:
Aberration is in agreement with about any feasible theory, as it agrees with both wave theories and particle theories of light. Your understanding that "relativity", that is, the Lorentz transformations does not "explain" aberration is mistaken. It is probably based on an error made by Einstein in his 1905 paper. When using the transformations of Lorentz, one has to compare the observations as made between two different "inertial frames" of observation, true or virtual. In relativity theory, when one changes speed one changes "frames". The two applicable frames are the frames of the earth at different times of the year, and not that of the earth and of a star where no observation is made.
More simply, at small velocities the relativity theory is indistinguishable from a standard ether theory. From that it follows directly that a change of velocity of the earth will affect the angle under which the light waves will be observed.
Reply
The error that Einstein made in his paper is basically the same as in the naïve derivation of the aberration of starlight in textbooks: you cannot vectorially add the speed of light to the speed of objects (Galilei transformation) because light has no reference frame in which it is at rest (invariance of c); Einstein mistakenly tried to solve this dilemma by applying the Galilei transformation nevertheless and then rescaling his space and time coordinates in order to at least have an invariant scalar value of c (see my pages regarding Relativity, Speed of Light and also the entry of Emory Taylor above for a more detailed treatment of this aspect).
Because light has no rest frame of its own, the velocity of the earth would therefore have to be referred to that of the star (just imagine that the star moves synchronously with the earth in an orbit of identical radius; then the earth and the star would be at rest relatively to each other and no aberration could possibly occur). However, if the propagation of light is truly independent of any motion of source or observer, it should only depend on the distance between them (as outlined on my Speed of Light page) and no aberration can occur at all.
As shown formally on my Aberration-page, even Einstein's (erroneous) transformation does not yield an aberration of starlight but merely a rotation of the star; one would need in fact a second Lorentz transformation at the observer to have an aberration effect.
Theoretically, an aberration of starlight appears therefore to be impossible to me, and one would have to look into possible observational errors that could suggest such an effect (e.g. seasonally varying telescope pointing errors, refraction effects etc.).
Why would an astronaut going out into space on a high speed rocket come back younger than us on earth? Wouldn't our light clocks on earth look slower to the traveling astronaut, just as his would look slower to us? Couldn't we as easily say that the rocket is stationary, and we on the earth are suddenly traveling the opposite direction?
Reply
Your example is known as the Twin Paradox and according to Relativity it is solved by the fact that the astronaut in the rocket is not in uniform motion but accelerated. The situation is therefore not symmetrical (after all, the rocket has to turn around to get back to the earth). This singles out the person in the rocket as the one who stays younger.
There have been experiments made with clocks on airplanes which show this effect and the argument used there is essentially the same. However, as indicated elsewhere on this site (see also Emory Taylor's comment above), the time dilation as such should in my opinion be impossible and the effect could be due to other physical influences affecting the rate of the atomic clock on board the aircraft (e.g. the effect of the earth's magnetic field; see my discussion with David Cooper).
For a purely uniform relative motion however the situation is obviously symmmetrical (as you said) and you would therefore have a paradox here if you apply the time dilation principle of relativity. However, as argued by me, the latter arises from the erroneous assumptions that a) light signals have to be used to define time (see also my discussion with Simon Pennington above) and b) that the speed of light can be added to the speed of objects in the usual way (i.e. vectorially). Kerry Brown (2)
So you couldn't just as easily say that the Earth (and the rest of the universe) is accelerating the opposite direction, while the rocket is staying still? Why isn't acceleration relative just as velocity is? I've always thought of acceleration as merely a measurement of the difference between two velocities in time. Is acceleration a properties of its own, and if so, how can something be considered to have an amount of acceleration at any one moment? Reply (2)
You are right, from a purely kinematic point of view (and Special Relativity is a purely kinematic theory) acceleration is as much a relative concept as velocity. It is not me who said that acceleration solves the Twin Paradox but proponents of the time dilation effect who try to find excuses for the logical inconsistencies of relativity (which I have addressed above). Some Relativists actually say that it is not the acceleration that resolves the Twin Paradox but the fact that one observer stays in his reference frame while the other changes reference frames (see http://www.phys.vt.edu/~jhs/faq/twins.html). However, it is obvious from the example given under this link that time dilation should already be there before the travelling twin turns around, so this argument doesn't hold either.
The thought experiment shown below does neither involve an acceleration nor a change of reference frame and proves therefore that time dilation is impossible:

A quote from the book RELATIVITY (Lawson tr.):The anomaly is the term 'naturally coincides'. We know that Einstein is assuming, along with Euclid, that the definition of the coincidence of two points is a point. However, we have never gotten a definition of a 'natural' coincidence of two points. We also have a problem if we try to resolve the issue ourselves. If we simply drop the 'naturally' we run into a situation in which Einstein has told us to assume two Cartesian coordinate systems, but now leaves us with one, since, following from the definition of the coincidence of two points, if two parallel coordinate systems coincide at one point, they coincide at all points and are one coordinate system, not two. We have been led to a contradiction.
'Are two events (e.g. the two strokes of lightning A and B) which are simultaneous with reference to the railway embankment also simultaneous relatively to the train? We shall show directly that the answer must be in the negative. When we say that the lightning strokes A and B are simultaneous with respect to be embankment, we mean: the rays of light emitted at the places A and B, where the lightning occurs, meet each other at the mid-point M of the length AB of the embankment. But the events A and B also correspond to positions A and B on the train. Let M1 be the mid-point of the distance AB on the traveling train. Just when the flashes (as judged from the embankment) of lightning occur, this point M1 naturally coincides with the point M but it moves towards the right in the diagram with the velocity v of the train.'
Reply
As indicated on my page regarding the Speed of Light, the 'simultaneity problem' is merely a consequence of the flawed assumption that the moment of detection of the light signal depends on the velocity of the train. The propagation of light has however to be independent of any relative movement of source and receiver, i.e. it can only depend on the distance of the two at the moment the light signal is emitted. The two lightning strokes DO therefore appear to be simultaneous not only on the embankment but also on the train. John Ryskamp (2)
Thanks. You know, I grappled with the issue you are mentioning, and I decided not to pursue it. This is why: I decided to consider relativity strictly as an argument, that is, as an intellectual structure the only rule for which is internal consistency. I realize that it did not answer the question: doesn't that diminish the potential applicability of the theory? But my goal was to discover whether, at a minimum or as a threshold, there was internal consistency--I put applicability to one side for the moment.
Thus, from that point of view, I simply did not reach the question of the issue of a 'flawed assumption' (and yours is not the only one people have claimed). From the point of view of strict internal consistency, there is no such thing as a flawed assumption, as I am sure you will agree. In argumentation, certain ideas play the role of assumptions. There is no rule that they be factually correct. The only rule is that they be logigally applied. You can assume that all cats are green if you want. You can assume anything, and then the question for the reader is whether your argument is consistent with your assumptions or whether it violates one of them. Reply (2)
I am sure you are aware that all logical conclusions are merely tautologies (i.e. statements that are always true by definition). If a theory is internally logically consistent, it is therefore impossible to draw factually right conclusions from factually wrong assumptions (premises). Factually wrong in Einstein's derivation of the Lorentz transformation formulae is the assumption that the speed of light adds vectorially to the speed of objects (as outlined on my page regarding the Speed of Light). Einstein tried to offset this circumstance by revising other premises (i.e. the definitions for the time and space units of measurement) but this does of course not render the conclusions as factually valid again (two separate inconsistencies do not result in consistency but merely in nonsense).
With regard to 'simultaneity', one should anyway note that this expression is in fact not properly defined: in the example mentioned in your first post, 'simultaneous' is merely referred to the moment of detection of the two light flashes, which obviously is not the same as the simultaneity of the events as such (i.e. the moments of the emission of the light flashes) (see also my discussion with Simon Pennington above in this context). It is not even necessary to define simultaneity using light signals, but if you do, you could define it by the condition that if point A and point B emit a light flash each, they are simultaneous if each point detects the flash from the other point at the same time. John Ryskamp (3)
I think that up to the 'natural' coincidence, we have not gotten to the stage where we are logically justified in asking whether he is factually wrong. He is at this stage still at the 'all cats are green' stage--that is, he is simply asking you to assume something, and that's a fair request.
Remember that he is only proposing his definition of simultaneity with respect to one cartesian coordinate system. He is not trying to establish or prove simultaneity. So up to that stage, it is fair to allow him to define simultaneity as he pleases. He is trying to prove, not simultaneity, but rather, the relativity of simultaneity. Simultaneity, and the relativity of simultaneity, are two separate concepts. Reply (3)
But the point is that the statement 'all cats are green' is factually wrong and hence any theory using this premise can not result in factually right conclusions. Einstein's assumption that the speed of light can be vectorially added to the speeds of objects is equally factually wrong and any theory using it must therefore also lead to flawed results. The alleged relativity of simultaneity is only one of these.
The point is that you can not just simply define or re-define concepts as you please, but you have to take care not to logically contradict existing, more fundamental concepts.