I've been reading about time dilation and the twin paradox lately, trying to achieve some kind of understanding of the various factors involved.
It seems to me that the experiments conducted with relativistic muons could shed some light on how one should treat wild claims of 'time travel' and 'a fountain of youth' stemming from space travel at speeds close to that of light.
As for cosmic muons lasting longer than they should, one possibility, that you have already mentioned, is simply that muons can travel faster than light. The speed of light may not apply to them. Muons are said to be examples of 'second generation matter' according to the Standard Model. The Earth, and everything on it, is first generation matter, and one can only speculate on how higher generation matter would behave in a lower generation matter environment. Neither SR nor GR mention the existence of such matter, suggesting that both theories only pertain to ordinary, first generation matter.
Another possibility, which has also already occurred to you, is that the muons are moving through the electric field of the atmosphere and/or the magnetic field of the Earth at very high speeds, which could have life-lengthening consequences for the particle in motion.
It's interesting that the cosmic muons are supposed to be the decay products of pions produced when cosmic protons hit the upper atmosphere. Pions should be subject to time dilation just as much as muons, yet it is only the muons that are detected at ground level. This leads me to wonder if no time dilation is occurring at all. Instead, all particles are decaying at their normal rates, but at varying heights in the atmosphere. In this model, for example, a relativistic cosmic proton happens to penetrate down to 2,000 feet above sea level. It collides with an air molecule, leading to the production of relativistic pions. Due to their short life (2.6 x 10^-8 seconds), these can only travel about 26 feet before decaying into relativistic muons. Our altitude is now 1,974 feet above sea level. The lifetime of the muon (2.2 microseconds) is much longer than that of the pion, so the muon can travel quite a way before decaying into a relativistic electron (2,164 feet, which would actually put the muon underground, in keeping with the detection of muons in deep mines). If the so-called muons are being 'detected' in terms of downward moving-electrons, which are the final products of pion decay, then obviously the initial point of interaction with the atmosphere can be moved to an even higher altitude. Some may scoff, but this view of muon production and decay would explain why there is now a solar flare warning system for airline pilots, which instructs them to reduce altitude when radiation levels in the atmosphere become excessive due to solar activity. If particle decay were only an edge-of-space phenomenon, then such a system would be unnecessary as incoming particles would be absorbed or slowed down before reaching altitudes where human activity occurs. In other words, the hazard from cosmic radiation may be greater than we've been led to believe, a state of affairs that shouldn't surprise anyone given the amount of money the global traveling public spends on flying every year.
Finally, it's amusing that the muons arrive at the surface of the Earth 'DOA'. If you must invoke time dilation to explain the presence of the muons in the first place, one must take note that this process appears to only 'stretch' (dilate?) the lifetime of the muon such that it can reach the ground, only to then decay. What isn't observed is a large population of fresh, young muons that start decaying only after reaching the Earth's surface. Applied to the twin paradox, this reasoning suggests that the twin that returns from a 2,000-L.Y. roundtrip (automated!) space voyage at 0.99c would be just as much of a skeleton as his Earthbound twin. This means, in turn, that interstellar travel, if it ever happens at all, would probably be limited to the very nearest stars, and any time dilation effect would merely enable the already elderly astronauts to die on Earth of old age shortly after disembarking. The idea that you could leave as a young man, return as a young man, and then live out the rest of your long life on Earth is really science fiction, and not supported by the data at all. For example, the muons in circular accelerator experiments live longer than their stationary counterparts, yes, but none are left over after their voyage. They still decay in route, and do not get to start living a new life once they have slowed back down terrestrial velocities. The time the muons spend in the accelerator is not timelessness. I suppose you could eke out some kind of miserable existence in an interstellar tin can, happy in a sort of perverse way that your life span is longer in some abstract sense than that of your coworkers left behind in Mission Control, but it makes more sense to me to achieve immortality in the usual way - through children and grandchildren!
Reply
Let me first emphasize that the twin paradox is a purely theoretical issue, which as such is completely unaffected by any experimental results. The theoretical claim is that a moving clock goes slower than an identical clock at rest just as a result of the relative velocity. If certain experiments (e.g. the muon experiments) appear to confirm that moving clocks go slower, then this still does not resolve any logical inconsistencies associated with this particular theoretical interpretation of the effect. Of course, you can always try to come up with alternative theoretical explanations, but lastly it has no impact on the question whether the 'time-dilation' explanation is a logically consistent one. Of course, like any physicist, I am interested in explaining observations, but these explanations would have to be conceptually and logically acceptable. The problem is that most (if not all) experiments regarding the clock rate in moving systems have only been specifically designed and evaluated to be compared to the relativistic theory. For any other explanation, there simply would not be the necessary additional information available to confirm or reject it. My personal feeling is that the magnetic field plays a crucial role here, especially as far as the muon experiments in synchrotrons are concerned (faster than light speeds can not really be assumed here, as those would lead to synchronization problems in the synchrotron; also, my own theory would predict that charged particles can not be accelerated beyond the speed of light by electric fields). But again, on the basis of presently available and published data, this is difficult to confirm or reject. Dedicated experiments or at least a dedicated re-analysis of existing data would be required here.
So let's get back to the crucial issue here, which is the logical consistency (or not) of the relativistic time dilation claim, as expressed through the 'twin paradox', which I have analyzed in detail on this page. In the paragraph 'Algebraic Time Dilation Paradox' there, I have indeed replicated Einstein's own derivation of time dilation in his 1905 paper (which is a purely mathematical consequence of the Lorentz transformation derived by him earlier in this paper). The point is that this derivation is only 'one-sided': Einstein calculates the clock rate of the moving clock as seen by the stationary observer, but he does not address the question how reversely the moving observer would see the clock rate of the stationary clock. This way, he simply avoids the twin paradox issue, which obviously would only become apparent if the roles of the two clocks are reversed. The only 'reversal' that Relativists consider here is to apply the back-transformation of the original Lorentz transformation, which obviously is always consistent with the original one, as the forward and inverse Lorentz transformation are algebraic identities (as is easy to show).
So what Relativists routinely do here is to apply the Lorentz transformation to data measured in one reference frame, then they transform these transformed (i.e. fictitious) data back from the other reference into the original one by means of the inverse Lorentz transformation, and since they (not surprisingly) obtain the original data again, they assume everything is consistent i.e. there is no paradox (it is somewhat similar to claiming that 1+1=3 is a true equation as it is consistent with 3-1=1).
It should be obvious that a twin paradox can only be obtained if the other (moving) observer can apply his own measurements of the clock rates in an exactly equivalent way. And as I have shown on my page, this clearly leads to a contradiction regarding the clock rates. Applied to the case of the atmospheric muons: if a ground observer finds that a fast moving atmospheric muon lives longer than a stationary ground based muon created at the same time, then reversely an observer moving with the atmospheric muon would find that a ground based muon created at the same time lives longer, Note that it is important here that in both cases the muons are created at the same time, because by definition distance measurements must involve simultaneous determinations of the coordinates. Now, according to the Lorentz transformation, simultaneous non-colocated events in one reference frame can not be simultaneous in another (moving) reference frame (this is to do with the length contraction, as illustrated in the diagram on the twin paradox page), so Relativity contradicts itself here. In other words, the relativistic time dilation (as well as length contraction) effect is logically flawed. Gerry Francisco (2)
Thanks so much for your reply. You have helped me to refine my position on relativity. Basically, I am now forced to believe that relativity is much ado about nothing. I will try to be as brief as possible, as my previous e-mails have been overly long. I'm going to look at only one accelerator experiment with pions, as I have data on this experiment, and all other relativity test experiments, such as Hafele-Keating and Pound-Rebka, would only lead to the same conclusions. My assumption at the outset is that relativity effects actually happen in the sense that they can be recorded with our senses and with our instruments, but that they are also illusory in that the actual test object wouldn't really, for example, contract, weigh more, and skip over certain amounts of time (it would only appear that way). In other words, let's assume that relativity is right, and show, using its own equations, that nothing of much importance stems from it.
The experiment consists of boosting a bunch of pions up to 0.75c with some kind of high-tech particle accelerator machine, and observing how far that they can get from the accelerator exit window before decaying. I have no choice but to assume that the experimenters can tell the pions apart from their decay products, but I really have no proof of this. Oh well. You can only do what you can do. Anyway, you can immediately see that this is basically a twin paradox experiment, with the pions serving as the starship and its crew.
The pion beam is observed to have a length of 8.8 meters. At that point, beta decay into other particles (muons, electrons) commences, but these are ignored, as we are only interested in the pions in this experiment.
Using L = L(0)*sqrt(1-v^2/c^2), where L(0) is the distance the pions traveled from the point of view of the experimenters, you can see that the pions "feel" that they have only traveled 5.85 meters. However, since no human being can know what a subatomic particle (or intrepid interstellar voyager) does or does not experience, this aspect of relativity (length contraction) doesn't seem to tell you very much about anything. So much for relativistic length contraction.
Using M = M(0)/sqrt(1-v^2/c^2), where M(0) is the rest mass of the pions as observed in the laboratory, you can see that the experimenters would say that the pions have a greater mass at 0.75c than at rest. However, as there is really no way to weigh an individual pion in a laser-like particle beam, just as there would be no way to weigh a distant starship, we find that once again we have an equation that doesn't really provide any useful information. So much for relativistic mass increase. True, you could put the pions in a magnetic field, to see how much their path curves, and from this deduce a mass, but then you could just say that it is the electric charge of the pion that is changing, and not the mass, leading once again to an unclear outcome that provides no useful information.
Using T = T(0)/sqrt(1-v^2/c^2), where T(0) is the apparent amount of time that the pions need to complete their journey, you can see that we have much the same problem that we had with length contraction. How can we say how much time that subatomic pions (or distant interstellar explorers) have experienced while in motion? The clever experimenters say that the lifetime of the pions (known to be 2.6 x 10^-8 s) acts as a kind of clock, and so this amount of time must have passed for them during their journey. Fair enough, but in all of the other relativity equations, one variable gives the actual quantity, while the other gives an apparent quantity. Therefore, if T(0) is apparent time, then T would have to be the actual amount of time required for pion decay, which works out to be 3.9 x 10^-8 s. If you stop here, and most people do, the math seems to be telling us that the pions, by moving at a substantial fraction of the speed of light, have had their lifetimes extended by a large factor, thus allowing them to travel to a more distant point in space than would ordinarily be allowed. This is the vaunted twin paradox, said to allow mankind to spread throughout the stars if we can only build ships that can move fast enough.
The problem is with the true nature of time: (apparent elapsed time) x (the factor by which time is slowed by motion) = (the true amount of elapsed time). On Earth, we perform this calculation automatically, since everyone has effectively agreed that time passes at a "speed" of 1.000000. Consequently, all elapsed times are true elapsed times. But, in an accelerator experiment, the high speeds "play" with time, but not in the way that you might think. The applicable relativity equation is T = T(0)*sqrt(1-v^2/c^2), where T gives the true rate at which time passes, while T(0) is just the apparent rate, which would always seem to be 1.000000 in any conceivable experiment since time is always going to seem to pass "normally" for "you". If "you" is a pion moving at 0.75c, then time would be slowed by a factor of 1.51. Multiplying the pion's apparent time by the factor by which time is slowed, you just get 3.9 x 10^-8 s, which is just the amount of time recorded in the accelerator laboratory for the pions to travel 8.8 m (D = R*T)! Therefore, there is no twin paradox, and all pions, whether moving or not, age at the same rate. You could say, then, that high speeds compress time periods, but decrease the rate at which time passes. The two effects cancel each other exactly, leaving one with the same amount of time that Earthbound observers would record. True, you could monitor your "starship time" with only a stopwatch-type clock that only records apparent elapsed time, but that would be a mistake, as you would be leaving out half of the temporal story.
So, by an elaborate mathematical route, we have just proven what we already suspected: time is the same for everyone, and cheating death via velocity is a pipe dream. Incidentally, it is dead (decayed) pions that arrive at the destination point, not energetic, youthful ones. By analogy, future space travelers would be in the same predicament - a ship of the dead arriving at an idyllic, new planet, unable to explore it due to their deceased condition.
To sum up, physics books and popular level TV science shows leave out the fact that there are two time dilation equations that need to be considered before making any fanciful predictions. Also, there is much confusion about what the variables in the equations really mean. Once all of this is cleared up, however, you find that there are no paradoxes and no free lunch.
But hasn't the lifetime of the pion been lengthened by a factor of 1.51 by traveling at 0.75c? Not necessarily, since we don't actually have any data from the same experimental apparatus that would allow us to figure out how far a pion beam would go if composed of pions traveling at a much slower speed. Instead, that distance is calculated for us. This is frequently, if not always, the case with pro-relativity experiments. Just saying. Reply (2)
Even Relativity does not claim that travelling fast makes you live longer. The so called 'proper time' is unaffected by the velocity. It is only that the distance to the destination planet becomes shorter due to the length contraction. So according to his clock, the traveller has spent less time getting there than according to the earth-based observer. The latter would have to assume instead that the traveller's clock (and his biological functions as well) have slowed down, thus enabling him to reach the planet alive (if the speed has been sufficiently high). Neither the travelling nor the earth (or planet) twin by himself has lived longer than he would have done anyway, it is just that the timelines of both have become disjointed, so effectively they are not twins anymore when they rejoin as they have now a different age.
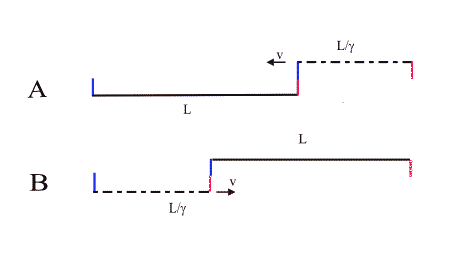
The essential factor for the timelines getting disjointed is the 'relativity of simultaneity' term in the Lorentz transformation equation for the time i.e. t'=γ(t-vx/c2) (this is the second term in the bracket, which makes the time transformation spatially dependent (this is what Einstein required to correct for the logical mistakes in his derivation). Depending on the scenario considered, this can not only lead to time dilation, but also to a sequence of events reversing its order (as in the thought experiment addressed on the twin paradox page). This is simply due to the observer dependent length contraction effect. I have illustrated it in the figure below: with the starting configuration as shown, the observer on rod A would see the red markers coincide first, then the blue markers, whereas the observer on rod B would see the events in the opposite order (the moving (and thus length-contracted rods are shown dashed-dotted).
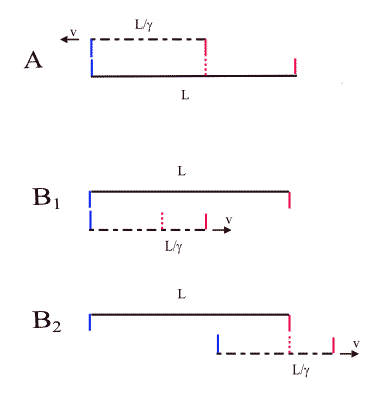
I think I am finally able to state my issue with SR briefly and succinctly:
Take the twin paradox. High speeds merely change our time units, not time itself. So, a space vehicle moving at 0.999999c would take only 1.41 Y (apparently) to reach a destination star system 1,000 L.Y. from Earth. This is only achieved by increasing the length of each second by a factor of 707.107. In other words, the extreme velocity of the ship has redefined the terrestrial time unit known as the second to now be 707.107 seconds in duration. Time itself, however, remains completely unaffected. Since clocks can only record time as they have been designed to record it (one second at a time), the ship's clock would only show that 1.41 Y have passed when the spaceship finally reaches the star. In reality, a full 1,000 Y would have passed, much to the detriment of the crew (1.41 Y x 707.107 = 1,000 Y).
It's the same with length contraction and mass increase. The applicable space (length, distance) and mass units have been redefined by velocity, but in reality nothing has changed.
Once again, SR = much ado about nothing.
GR is probably the same: gravity merely redefines the same three units of space, mass, and time, just like velocity did for SR, while actual space, mass, and time remain the same as they always were.
Einstein's mistake in a nutshell: Confusing measurements performed on a thing with the thing itself. Reply (3)
Relativity would claim that the ship crew gets to the destination star in 1.41 Y (ship time), but on the star 1,000 Y have passed since they started from earth. So like I said, the timelines of the two become disjointed, to a point where in practice the whole trip becomes meaningless (imagine the star sends out some distress signal, calling for help from earth: first of all, it would take 1000 years for this call to reach the earth, and then another 1000 years for the ship to arrive there; even though the crew will have got there in 1.41 years, the call will by then be utterly irrelevant, as the civilization will not exist anymore in the form when the call was made. Of course, if it would just be a matter to be able to get to far away locations in order to explore or habitate them, it would make sense (although it would practically be a no-return mission).
However, these are anyway merely fantasies without any valid scientific basis: as I indicated before, the Lorentz transformation (on which these fantasies are based) is logically inconsistent. I have tried to illustrate this in the diagram below for the case of the muon example (which you addressed originally): in the earth's frame, the time for the muon to reach the surface is T=h/v; according to the Lorentz transformation, the time should be a factor 1/γ shorter in the muons frame (explained by the length contraction of the height h in that frame). But if you now reversely get the earth time back from this (you can either read it off the graphic or algebraically do the Lorentz transformation), you find that this again is a factorγ shorter than the muon time, i.e. we would have T=h/v/γ2, which obviously is a mathematical contradiction to the original assumption (unless γ=1 i.e. v=0).
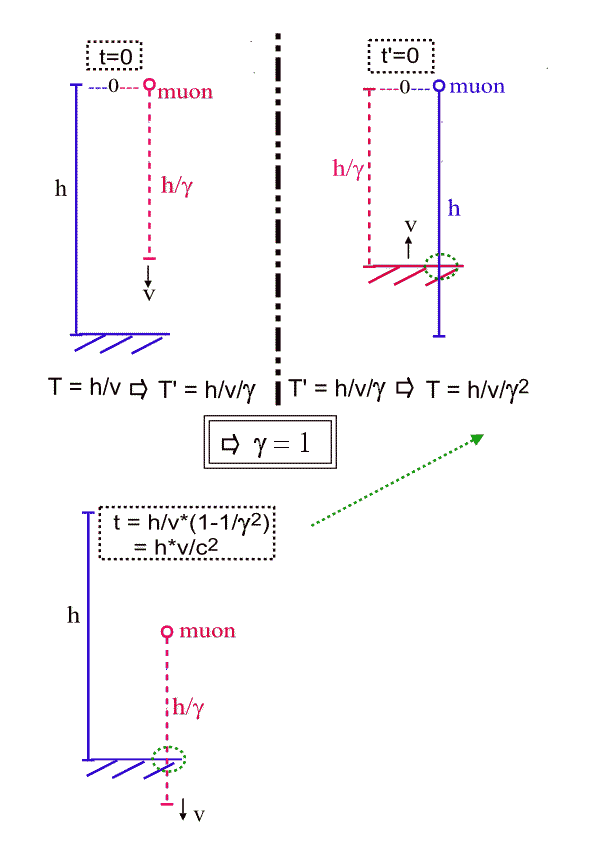
So just to emphasize this again, the 'twin paradox' is ingrained in the Lorentz transformation itself, and not a result of an incomplete understanding/application of the latter (as Relativists usually claim). On the contrary, the 'resolutions' of the twin paradox given by Relativists are themselves contradictory and flawed. In this sense, any practical discussion of how to interpret certain time dilation or length contraction scenarios are meaningless. Gerry Francisco (4)
I think I get what you are saying, although I found it easier to return to the pion example, since the shorter distances found there made things easier to visualize than in the muon example.
The beam of pions is basically a "stick" or "rod" moving at 0.75c. A stationary observer seeing this beam will see it as length-contracted, according to SR. In the pion example, this observed distance was 8.8 meters. Using the Lorentz transformation for lengths, the "true" length for the beam would have to be 13.3 meters. But, according to D = R*T, the length of the beam in a Newtonian world should be only 5.85 meters. Therefore, whether you use the experimental length or the "true" corrected length, the beam has actually suffered a length expansion, exactly the opposite effect that SR says should occur, thus suggesting that the whole affair is nonsense and a house of cards. Reply (4)
It seems you are mixing something up here with regard to the length contraction/expansion: 'length contraction' relates to the ratio (apparent length)/(true length). Of course, for the ratio (true length)/(apparent length) it would be an expansion, but that would only be consistent. The inconsistency only comes in when taking the 'true length' in the other reference frame: then the length contraction would be reversed (as indicated in the drawings above), which would lead to the 'twin paradox' type of contradictions.
The point is that the inverse Lorentz transformation does actually not refer to coordinate measurements made in the second reference frame. It is just the back-transformation of the transformed coordinates made in the first reference frame (the forward and backward Lorentz transformation are algebraic identities, as is easy to show). So Relativity can only be 'consistent' if it does not allow the second (moving) observer to make his own measurements but instead tells the latter what data to use on the basis of the measurements of the first observer (which, like I said above already, is similar to saying that 1+1=3 is correct as it is consistent with 3-1=1).
About six years ago I stopped believing that time dilation was possible. I knew that it went against common sense but we were told that even though it did go against common sense, that was the way it was. One day my brain just said, no actually in this situation common sense is correct and it is impossible.
I started questioning a number of things but it took me six years to question one of the most fundamental beliefs in the science world and that is that the speed of light is invariant.
But then I realised something which really took me by surprise because it was so obvious. The Michelson-Morley experiment does not have a moving observer, so I realised that we don't have any experiments which show that the speed of light is invariant.
I have asked that question in a physics forum and my post was removed.
Could you please tell me your thoughts.
Reply
The Michelson-Morley experiment was based on the assumption that the speed of light refers to some medium (the so called 'ether'). In that case it would have detected any motion relative to this ether (which it didn't). Of course, the assumption of an ether is a contradiction in terms if one considers light propagation in a vacuum. In contrast to other waves (e.g. sound waves, water waves) light does in fact not need any carrier medium as it carries itself (according to Maxwell's equations, the electric wave carries the magnetic wave and vice versa). In this case, the speed could only depend on the relative motion of the source and detector, but as those are stationary with regard to each other in the Michelson-Morley experiment, it could obviously not detect anything. But there are other experiments and observations which prove that the speed of light does not depend on the speed of the observer relative to the light source (for instance the observation of double stars). On my page regarding the speed of light, I have also given a theoretical argument why it must be constant (see the second paragraph below the box on this page).
Whilst the constancy of the speed of light in a vacuum is in this sense well proven, the alleged consequence of it, the theory of Special Relativity, is however an erroneous conclusion. I have discussed this in detail on my page regarding the light speed postulate and its interpretation
For some years I've considered that Einstein's theory that gravity warps space and time is incorrect. In my opinion if this were actually true then matter would have nothing consistent to pass through.
I therefore interpret the theory a little differently. In my understanding there would be two concepts of time. One would be a sort of constant time that is the same over the entire universe (for every second that passes in one location, a second passes in every other location). The other is a sort of gravity dependent time (the more gravity there is the slower time goes because there is a sort of friction between matter and gravity that slows things down).
That's my first topic, where I'd just like to ask 'Is that how it works functionally?'
My second question is more of a age of the universe problem, as physics might come into it.
General scientific estimates place the age of the world as millions and billions of years. There are two main things that make it hard to argue with such estimates, these are (1) light from distant stars couldn't have travelled the distance in a lesser amount of time and (2) radioactive decay of elements theoretically provide accurate dating.
I take an alternative theory. In my theory light would initially have travelled at an uninhibited rate and then have gradually slowed as energy in inhibiting bands built up. Therefore a star would initially have given off light and energy in what we might call band A. Band A energy would get in the way of and inhibit light (but only slightly). The original energy in band A would eventually (say over 1000 years) go down in energy to form a band B. Taking it further one could suppose to date that there are bands a, b, c, d, e, and f, all inhibiting the speed of light and that the world is only thousands of years old. Presumably anything falling below band f loses charge and becomes inert.
In terms of radioactive decay I would presume an originally uninhibited level of decay, with it being gradually slowed by (possibly the same) energy bands as in the light discussion. This would therefore account for possibly large overestimates for the age of fossils, and whether it could explain different radioisotopes giving different ages for the same sample involves a bit more science than I'd be concerned with.
I therefore ask regarding this part of my message, Is there anything known to physics that would support this theory of different energy bands? (as you're probably in a better position to know than I am).
Reply
First of all, the concept of 'time' is often misunderstood, even (or in particular) by physicists: time is actually not a physical entity as such but something that we derive from observed changes in physical systems. Those changes that occur with some regularity we tend to use as time standards, e.g. the planetary motions, mechanical clocks or atomic clocks. It is not possible to speak of time without (at least implicitly) relating to these physical time standards. Of course, your particular time piece is not really an exactly accurate standard. Your clock may go slow or fast because of any number of physical influences, e.g. temperature, your battery running low etc.. The fact that a particular clock is not a true time standard does of course not mean that time goes slower or faster. Likewise, the fact that a clock goes slower in a gravitational field does not mean that time goes slower. It only means that we can't use that particular clock as a time standard anymore without making appropriate corrections for it. Clocks of a different construction may well be less affected by gravity.
As for your 'energy band' suggestions for the speed of light and radioactive decay:
the energy of light does actually per se not change during travel, neither its speed. Assuming it travels in a perfect vacuum, there is nothing that could affect either of them.
The radioactive decay on the other hand can only be described as a statistical process. As an analogy, imagine many air molecules bouncing around in a box that has a very small hole in one of its walls. Occasionally, you will have one molecule escaping through the hole. The statistical probability for that is the same for each molecule (given by the ratio of the area of the hole to that of the total wall surface) but obviously some molecules will escape earlier than others (depending on when they manage to hit the hole). Similarly, all radioactive nuclei of the same element have the same probability of decaying within a certain time (as given by their half-life time) but some decay earlier and some later. The probability only changes from element to element (in our analogy this would correspond to the hole in the wall having a different size) but it does not change with time (the size of the hole in the wall does not change with time). At least that is what experiments show. If radio-dating gives different ages using different elements, then this is most likely due to either the sample for one of the elements not being large enough (so the statistical accuracy is low) or the sample has been contaminated at a later time with one of the elements.
If time slows as an object increases velocity wouldn't that indicate that time is object specific? And if the speed of light is a constant and does not change regardless of the velocity of an object wouldn't that indicate that time used to measure the speed of light changes? The video I have posted at the this link graphically depicts the questions asked.
Reply
Your video gives indeed a qualitative explanation how the conclusion of time dilation is reached in the theory of relativity. However, the argument (as well as that of Einstein in his original derivation) suffers from a fundamental flaw: it is actually not possible to relate the position of the light signal to that of the observers as you have done it without violating/misinterpreting the principle of the invariance of the speed of light. You can find this explained in detail on this page. The conclusions of relativity (including time dilation) are therefore invalid.